题目内容
18.将函数$y=4sin({4x+\frac{π}{6}})$的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将所得图象向右平移$\frac{π}{6}$个单位,则所得函数图象的一个对称中心为( )| A. | (0,0) | B. | $({\frac{π}{3},0})$ | C. | $({\frac{π}{12},0})$ | D. | $({\frac{5}{8}π,0})$ |
分析 利用y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再利用正弦函数的图象的对称性求得g(x)图象的一个对称中心.
解答 解:将函数$y=4sin({4x+\frac{π}{6}})$的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),
可得y=4sin(2x+$\frac{π}{6}$)的图象;
再将所得图象向右平移$\frac{π}{6}$个单位,可得函数y=4sin(2x-$\frac{π}{6}$)的图象,
令2x-$\frac{π}{6}$=kπ,求得x=$\frac{kπ}{2}$+$\frac{π}{12}$,可得g(x)的一个对称中心为($\frac{π}{12}$,0),
故选:C.
点评 本题主要考查y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.若直线过点(1,2),(4,2+$\sqrt{3}$)则此直线的倾斜角是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
13.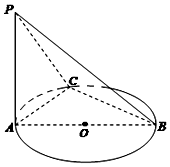 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
3.函数y=lg(sin2x)+$\sqrt{9-{x^2}}$的定义域是( )
| A. | [-3,3] | B. | (0,$\frac{π}{2}$) | C. | [-3,-$\frac{π}{2}$)∪(0,$\frac{π}{2}$) | D. | (-3,-$\frac{π}{2}$)∪(0,$\frac{π}{2}$) |
7.$若f(n)=tan\frac{nπ}{3},(n∈{N^*}),则f(1)+f(2)+…+f(2017)$=( )
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 0 | D. | $-2\sqrt{3}$ |