题目内容
10.棱长为1的正方体截去一部分之后余下的几何体,其三视图如图所示,则余下几何体体积的最小值为( )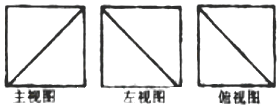
| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
分析 先根据题目所给的几何体的三视图得出该几何体的直观图,然后计算该几何体的体积即可.
解答 解:从三视图可知,截面一定是沿着各面对角线切割正方体的,图1所示是其中一种情况,即截去一个直角三棱锥,但所求的几何体的体积是最大的,为1-$\frac{1}{3}$×$\frac{1}{2}$=$\frac{5}{6}$,
而当正方体中截去两个这样的直角三棱锥如图2,余下几何体ABD-B1C1D1时,体积最小,为$\frac{2}{3}$.
故选C.
点评 本题考查立体几何中的三视图和空间想象力,考查数形结合思想,属于中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
13.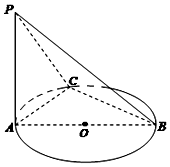 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
18.直线x+2y=m(m>0)与⊙O:x2+y2=5交于A,B两点,若|${\overrightarrow{OA}$+$\overrightarrow{OB}}$|>2|${\overrightarrow{AB}}$|,则m的取值范围是( )
| A. | $({\sqrt{5},2\sqrt{5}})$ | B. | $({2\sqrt{5},5})$ | C. | $({\sqrt{5},5})$ | D. | $({2,\sqrt{5}})$ |
5.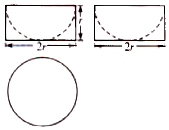 一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )
一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )
 一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )
一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )| A. | 27π | B. | 36π | C. | 45π | D. | 54π |
2.一个几何体的三视图如图所示,其中俯视图为正方形,则最长侧棱(不包括底面的棱)的长度为( )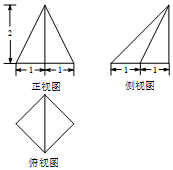

| A. | 2 | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
19.某几何体的三视图如图所示,则该几何体的体积为( )
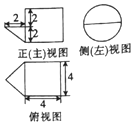

| A. | 6π | B. | $\frac{46}{3}$π | C. | 18π | D. | $\frac{52}{3}$π |
20.函数$f(x)=\sqrt{x+1}+lg(x-3)$的定义域是( )
| A. | [-1,3) | B. | (-∞,-1] | C. | [3,+∞) | D. | (3,+∞) |