题目内容
已知各项不相等的数列{an}中，an+2=
，求证：{an+1-an}是等比数列．
| an+an+1 |
| 2 |
考点：数列递推式
专题：等差数列与等比数列
分析：根据等比数列的定义，利用构造法即可证明数列{an+1-an}是等比数列；
解答：
解：an+2=
，
所以2an+2=an+an+1，可得an+2-an+1=-
（an+1-an）．
∴
=-
，
满足等比数列的定义，{an+1-an}是以-
为公比的等比数列
∴{an+1-an}是等比数列．
| an+an+1 |
| 2 |
所以2an+2=an+an+1，可得an+2-an+1=-
| 1 |
| 2 |
∴
| an+2-an+1 |
| an+1-an |
| 1 |
| 2 |
满足等比数列的定义，{an+1-an}是以-
| 1 |
| 2 |
∴{an+1-an}是等比数列．
点评：本题主要考查等比数列的证明，数列递推关系式的应用，是解决本题的关键．要求熟练掌握转化技巧．
练习册系列答案
相关题目
已知函数f（x）=[ax2+（a-1）2x+a-（a-1）2]ex（其中a∈R）．
（1）若x=0为f（x）的极值点，求a得值；
（2）在（1）的条件下，解不等式f（x）＞（x-1）（
x2+x+1）．
（1）若x=0为f（x）的极值点，求a得值；
（2）在（1）的条件下，解不等式f（x）＞（x-1）（
| 1 |
| 2 |
若将函数y=sin（ωx+
）（ω＞0）的图象向左平移
个单位，与函数y=sin（ωx+
）的图象重合，则ω的最小值为（ ）
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
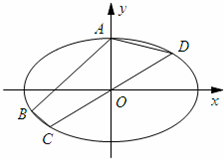已知椭圆G：