题目内容
已知:n∈Z,f(n)=cos(
π+θ)+cos(
π-θ).
(1)分别求出f(1),f(2),f(3),f(4)的值;
(2)猜想f(2k-1),f(2k)(k∈Z)的表达式,并对猜想的结果进行验证.
| 3n+1 |
| 3 |
| 3n-1 |
| 3 |
(1)分别求出f(1),f(2),f(3),f(4)的值;
(2)猜想f(2k-1),f(2k)(k∈Z)的表达式,并对猜想的结果进行验证.
考点:归纳推理,运用诱导公式化简求值
专题:计算题,三角函数的图像与性质,推理和证明
分析:(1)将1,2,3,4代入f(n)=cos(
π+θ)+cos(
π-θ)求出f(1),f(2),f(3),f(4);
(2)猜想f(2k-1)=-2cos(
π+θ),f(2k)=2cos(
π+θ),(k∈Z);利用三角恒等变换化简.
| 3n+1 |
| 3 |
| 3n-1 |
| 3 |
(2)猜想f(2k-1)=-2cos(
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:(1)f(1)=cos(π+
π+θ)+cos(π-
π-θ)=-2cos(
π+θ),
f(2)=cos(2π+
π+θ)+cos(2π-
π-θ)=2cos(
π+θ),
f(3)=cos(3π+
π+θ)+cos(3π-
π-θ)=-2cos(
π+θ),
f(4)=cos(4π+
π+θ)+cos(4π-
π-θ)=2cos(
π+θ);
(2)猜想f(2k-1)=-2cos(
π+θ),f(2k)=2cos(
π+θ),(k∈Z);
证明如下:
f(2k-1)=cos((2k-1)π+
π+θ)+cos((2k-1)π-
π-θ)
=cos(-π+
π+θ)+cos(-π-
π-θ)
=-2cos(
π+θ),
f(2k)=cos(2kπ+
π+θ)+cos(2kπ-
π-θ)
=cos(
π+θ)+cos(-
π-θ)
=2cos(
π+θ).
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
f(2)=cos(2π+
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
f(3)=cos(3π+
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
f(4)=cos(4π+
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)猜想f(2k-1)=-2cos(
| 1 |
| 3 |
| 1 |
| 3 |
证明如下:
f(2k-1)=cos((2k-1)π+
| 1 |
| 3 |
| 1 |
| 3 |
=cos(-π+
| 1 |
| 3 |
| 1 |
| 3 |
=-2cos(
| 1 |
| 3 |
f(2k)=cos(2kπ+
| 1 |
| 3 |
| 1 |
| 3 |
=cos(
| 1 |
| 3 |
| 1 |
| 3 |
=2cos(
| 1 |
| 3 |
点评:本题考查了归纳推理的应用及三角恒等变换的应用,属于基础题.

练习册系列答案
相关题目
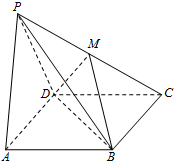 如图,四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD.