题目内容
已知函数f（x）=lgsin（
-2x），求函数的定义域、值域以及其单调增区间．
| π |
| 3 |
考点：复合三角函数的单调性
专题：计算题,函数的性质及应用,三角函数的图像与性质
分析：要使函数有意义，则有sin（
-2x）＞0，解得，即可得到定义域；由于0＜sin（
-2x）≤1，即可得到值域；根据复合函数的单调性，运用正弦函数的单调减区间，即可得到所求的单调增区间．
| π |
| 3 |
| π |
| 3 |
解答：
解：函数f（x）=lgsin（
-2x），
则有sin（
-2x）＞0，即sin（2x-
）＜0，
则2kπ+π＜2x-
＜2kπ+2π，即有kπ+
＜x＜kπ+
，k为整数．
则定义域为（kπ+
，kπ+
），k为整数；
由于0＜sin（
-2x）≤1，则y≤0，即有值域为（-∞，0]；
由于y=sin（
-2x）=-sin（2x-
），
可求函数y的减区间，
令2kπ+
≤2x-
≤2kπ+
，解得，kπ+
≤x≤kπ+
，
结合定义域，可得，有kπ+
＜x≤kπ+
，
则有单调增区间为（kπ+
，kπ+
]．k为整数．
| π |
| 3 |
则有sin（
| π |
| 3 |
| π |
| 3 |
则2kπ+π＜2x-
| π |
| 3 |
| 2π |
| 3 |
| 7π |
| 6 |
则定义域为（kπ+
| 2π |
| 3 |
| 7π |
| 6 |
由于0＜sin（
| π |
| 3 |
由于y=sin（
| π |
| 3 |
| π |
| 3 |
可求函数y的减区间，
令2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| 5π |
| 12 |
| 11π |
| 12 |
结合定义域，可得，有kπ+
| 2π |
| 3 |
| 11π |
| 12 |
则有单调增区间为（kπ+
| 2π |
| 3 |
| 11π |
| 12 |
点评：本题考查对数函数的性质及正弦函数的性质和运用，考查基本三角不等式的解法，考查运算能力，属于中档题和易错题．
练习册系列答案
相关题目
已知集合A={x∈N|x＜6}，则下列关系式错误的是（ ）
| A、0∈A | B、1.5∉A |
| C、-1∉A | D、6∈A |
函数f（x）当x趋近于x0时极限存在是f（x）在点x0的某个去心领域内有界的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、即不充分也不必要条件 |
如图，空间四边形ABCD中，各边及对角线长均为2，E是AB的中点，过CE且平行于AD的平面交BD于F，则△CEF的面积为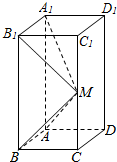
如图所示，在长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，M是棱CC1的中点．