题目内容
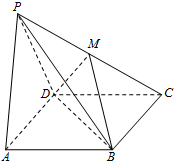如图，四棱锥P-ABCD中，底面ABCD为矩形，平面PAD⊥平面ABCD．（1）求证：AB⊥PD；
（2）若M为PC的中点，求证：PA∥平面BDM．
考点：直线与平面平行的判定,空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：（1）根据面面垂直，得线面垂直，再证明线线垂直；
（2）在平面BDM内找与PA平行的直线即可．
（2）在平面BDM内找与PA平行的直线即可．
解答：
证明：（1）∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，
又底面ABCD为矩形，
∴AB⊥AD
∴AB⊥平面PAD，
又PD?平面PAD，
∴AB⊥PD；
（2）AC与BD的交点E，连结ME，
∵底面ABCD为矩形，
∴E为AC的中点，
又M是AC的中点，
∴ME∥PA，
又PA?平面BDM，ME?平面BDM，
∴PA∥平面BDM．
又底面ABCD为矩形，
∴AB⊥AD
∴AB⊥平面PAD，
又PD?平面PAD，
∴AB⊥PD；
（2）AC与BD的交点E，连结ME，
∵底面ABCD为矩形，
∴E为AC的中点，
又M是AC的中点，
∴ME∥PA，
又PA?平面BDM，ME?平面BDM，
∴PA∥平面BDM．
点评：本题主要考查线面垂直的判定与性质，线面平行的判定与性质．
练习册系列答案
阅读快车系列答案
相关题目
如图中阴影部分所表示的集合是（ ）
| A、B∩[∁U（A∪C）] |
| B、（A∪B）∪（B∪C） |
| C、（A∪C）∩（∁UB） |
| D、[∁U（A∩C）]∪B |
已知集合A={x∈N|x＜6}，则下列关系式错误的是（ ）
| A、0∈A | B、1.5∉A |
| C、-1∉A | D、6∈A |
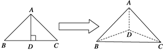如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，则下列四个结论中错误的是（ ）| A、BD⊥AC | ||
| B、△ABC是等边三角形 | ||
| C、平面ADC⊥平面ABC | ||
D、二面角A-BC-D的正切值为
|
如图，三棱柱的侧棱长为2，底面是边长为2的正三角形，AA1⊥面A1B1C1，正视图是边长为2正方形．函数f（x）当x趋近于x0时极限存在是f（x）在点x0的某个去心领域内有界的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、即不充分也不必要条件 |