题目内容
正四棱台两底面边长分别为3cm和5cm，那么它的中截面（平行于两底面且与两底面距离相等的截面）的面积为 ．
考点：棱柱、棱锥、棱台的侧面积和表面积
专题：空间位置关系与距离
分析：设已知正四棱台ABCD-A1B1C1D1中，A′，B′，C′，D′分别为侧棱的中点，将四条侧棱延长，交于一点P，则A1B1∥AB，△PA1B1∽△PAB，相似比为
，由此能求出正四棱台的中截面的面积．
| 3 |
| 5 |
解答：
解：∵正四棱台两底面A1B1C1D1和ABCD的边长分别为3cm和5cm，
∴
=
，
设已知正四棱台ABCD-A1B1C1D1中，
A′，B′，C′，D′分别为侧棱的中点，
将四条侧棱延长，交于一点P，
则A1B1∥AB，△PA1B1∽△PAB，相似比为
，
∴
=
，∴
=
，
设PA1=3a，则A1A=2a，A1A′=a，PA′=4a，
∴△PA1B1∽△PA′B′，相似比为
=
=
，
∵S正方形A1B1C1D1=3×3=9，
∴S正方形A′B′C′D′ =4×4=16．
∴正四棱台的中截面的面积为16cm2．
故答案为：16cm2．
∴
| A1B1 |
| AB |
| 3 |
| 5 |
设已知正四棱台ABCD-A1B1C1D1中，
A′，B′，C′，D′分别为侧棱的中点，
将四条侧棱延长，交于一点P，
则A1B1∥AB，△PA1B1∽△PAB，相似比为
| 3 |
| 5 |
∴
| PA1 |
| PA |
| 3 |
| 5 |
| PA1 |
| A1A |
| 3 |
| 2 |
设PA1=3a，则A1A=2a，A1A′=a，PA′=4a，
∴△PA1B1∽△PA′B′，相似比为
| PA1 |
| PA′ |
| 3a |
| 4a |
| 3 |
| 4 |
∵S正方形A1B1C1D1=3×3=9，
∴S正方形A′B′C′D′ =4×4=16．
∴正四棱台的中截面的面积为16cm2．
故答案为：16cm2．
点评：本题考查正四棱台的中截面的面积的求法，是中档题，解题时要注意空间思维能力的培养．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
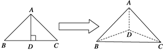如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，则下列四个结论中错误的是（ ）| A、BD⊥AC | ||
| B、△ABC是等边三角形 | ||
| C、平面ADC⊥平面ABC | ||
D、二面角A-BC-D的正切值为
|
如图，空间四边形ABCD中，各边及对角线长均为2，E是AB的中点，过CE且平行于AD的平面交BD于F，则△CEF的面积为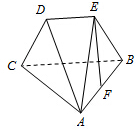
在多面体ABCDE中，BC=BA，DE∥BC，AE⊥平面BCDE，BC=2DE，F为AB的中点．