题目内容
数列{an}满足a1=
,an∈(-
,
),且tanan+1•cosan=1(n∈N*).
(Ⅰ)证明数列{tan2an}是等差数列,并求数列{tan2an}的前n项和;
(Ⅱ)求正整数m,使得11sina1•sina2•…•sinam=1.
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
(Ⅰ)证明数列{tan2an}是等差数列,并求数列{tan2an}的前n项和;
(Ⅱ)求正整数m,使得11sina1•sina2•…•sinam=1.
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由于对任意正整数n,an∈(-
,
),且tanan+1•cosan=1(n∈N*).可得tan2an+1=
=1+tan2an,即可证明数列{tan2an}是等差数列,再利用通项公式及其前n项和公式即可得出.
(II)由cosan>0,tanan+1>0,an+1∈(0,
).可得tanan,cosan,利用同角三角函数基本关系式可得sina1•sina2•…•sinam=(tana2•cosa1)•(tana3cosa2)•…•(tanam•cosam-1)•(tana1•cosam)=(tana1•cosam),即可得出.
| π |
| 2 |
| π |
| 2 |
| 1 |
| cos2an |
(II)由cosan>0,tanan+1>0,an+1∈(0,
| π |
| 2 |
解答:
(Ⅰ)证明:∵对任意正整数n,an∈(-
,
),且tanan+1•cosan=1(n∈N*).
故tan2an+1=
=1+tan2an,
∴数列{tan2an}是等差数列,首项tan2a1=
,以1为公差.
∴tan2an=
+(n-1)×1=
.
∴数列{tan2an}的前n项和=
n+
=
n2-
n.
(Ⅱ)解:∵cosan>0,∴tanan+1>0,an+1∈(0,
).
∴tanan=
,cosan=
,
∴sina1•sina2•…•sinam=(tana1cosa1)•(tana2•cosa2)•…•(tanam•cosam)
=(tana2•cosa1)•(tana3cosa2)•…•(tanam•cosam-1)•(tana1•cosam)
=(tana1•cosam)=
•
=
,
由
=
,得m=40.
| π |
| 2 |
| π |
| 2 |
故tan2an+1=
| 1 |
| cos2an |
∴数列{tan2an}是等差数列,首项tan2a1=
| 1 |
| 3 |
∴tan2an=
| 1 |
| 3 |
| 3n-2 |
| 3 |
∴数列{tan2an}的前n项和=
| 1 |
| 3 |
| n(n-1) |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
(Ⅱ)解:∵cosan>0,∴tanan+1>0,an+1∈(0,
| π |
| 2 |
∴tanan=
|
|
∴sina1•sina2•…•sinam=(tana1cosa1)•(tana2•cosa2)•…•(tanam•cosam)
=(tana2•cosa1)•(tana3cosa2)•…•(tanam•cosam-1)•(tana1•cosam)
=(tana1•cosam)=
| ||
| 3 |
|
|
由
|
| 1 |
| 11 |
点评:本题考查了等差数列的通项公式及其前n项和公式、同角三角函数基本关系式,考查了推理能力与计算能力,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若直线y=x+b与曲线x=
有且只有一个交点,则b的取值范围是( )
| 1-y2 |
A、|b|=
| ||
| B、-1<b≤1 | ||
C、-1<b≤1或b=-
| ||
| D、以上答案都不对 |
 如图,梯形ABCD中,AB∥CD,且AB=2CD,对角线AC、DB相交于点O.若
如图,梯形ABCD中,AB∥CD,且AB=2CD,对角线AC、DB相交于点O.若| AD |
| a |
| AB |
| b |
| OC |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
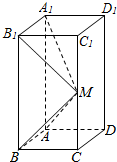 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点.
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点.