题目内容
设a，b，c为不全相等的正数，求证：
+
+
＞3．
| a+c-b |
| b |
| a+b-c |
| c |
| b+c-a |
| a |
考点：不等式的证明
专题：推理和证明
分析：依题意，利用基本不等式可得
+
≥2，
+
≥2，
+
≥2，又a，b，c为不全相等的正数，于是有
+
+
+
+
+
＞6，整理后即证得结论成立．
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
解答：
证明：∵a，b，c为正数，
∴
+
≥2，
+
≥2，
+
≥2，
又a，b，c为不全相等的正数，
∴
+
+
+
+
+
＞6，
∴
+
+
-3＞3，
∴
+
+
＞3（得证）．
∴
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
又a，b，c为不全相等的正数，
∴
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
∴
| a+c |
| b |
| a+b |
| c |
| b+c |
| a |
∴
| a+c-b |
| b |
| a+b-c |
| c |
| b+c-a |
| a |
点评：本题考查不等式的证明，着重考查基本不等式的应用，考查等价转化思想与推理、变形能力，属于中档题．
练习册系列答案
相关题目
已知集合A={x∈R|x2-2x-3＜0}，B={x∈R|-2＜x＜2}，则A∩B=（ ）
| A、（-1，1） |
| B、（-1，2） |
| C、{-1，0} |
| D、{0，1} |
已知全集A={3，4，5}，B={1，3，6}，则A∩B=（ ）
| A、{3} |
| B、{4，5} |
| C、{1，6} |
| D、{2，4，5，7} |
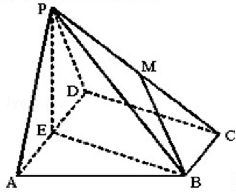如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，E为AD中点，M是棱PC的中点，PA=PD=2，BC=函数f（x）=-x3-2x2+4x，当x∈[-3，3]时，有f（x）≥m2-14m恒成立，则实数m的取值范围是（ ）
| A、（-3，11） |
| B、（3，11） |
| C、[3，11] |
| D、[2，7] |