题目内容
已知双曲线C：
-
=1以C的右焦点为圆心，且与C的渐近线相切的圆的半径是 ．
| x2 |
| 3 |
| y2 |
| 2 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：先求出双曲线C：
-
=1的右焦点和渐近线，从而得到圆的圆心和半径．
| x2 |
| 3 |
| y2 |
| 2 |
解答：
解：双曲线
-
=1的右焦点为（
，0），
渐近线方程是
x±
y=0，
∴半径r=
=
，
故答案为：
．
| x2 |
| 3 |
| y2 |
| 2 |
| 5 |
渐近线方程是
| 2 |
| 3 |
∴半径r=
| ||
|
| 2 |
故答案为：
| 2 |
点评：本题考查圆锥曲线的性质和应用，解题时认真审题，注意公式的合理运用．
练习册系列答案
相关题目
已知全集A={3，4，5}，B={1，3，6}，则A∩B=（ ）
| A、{3} |
| B、{4，5} |
| C、{1，6} |
| D、{2，4，5，7} |
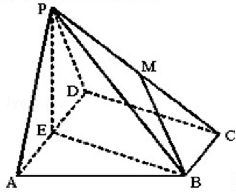如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，E为AD中点，M是棱PC的中点，PA=PD=2，BC=函数f（x）=-x3-2x2+4x，当x∈[-3，3]时，有f（x）≥m2-14m恒成立，则实数m的取值范围是（ ）
| A、（-3，11） |
| B、（3，11） |
| C、[3，11] |
| D、[2，7] |