题目内容
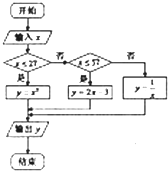若程序框图如图所示，视x为自变量，y为函数值，可得函数y=f（x）的解析式，那么函数f（x）-4在x∈R上的零点个数为（ ）| A、2 | B、3 | C、4 | D、5 |
考点：程序框图
专题：函数的性质及应用,算法和程序框图
分析：由程序框图可确定此程序框图的算法功能为求分段函数的值，根据判断框的条件列出每段的解析式，从而得到函数y=f（x）的解析式，在各段中令f（x）-4=0解方程，从而求出函数f（x）-4在x∈R上的零点个数．
解答：
解：当x≤2时，y=x2；
当2＜x≤5时，y=2x-3；
当x＞5时，y=
；
∴y关于x的函数解析式为y=
；
∴当x≤2时，令f（x）-4=x2-4=0，可解得x=2或x=-2；
当2＜x≤5时，令f（x）-4=2x-3-4=0，可解得x=3.5；
当x＞5时，令f（x）-4=
-4=0，x无解．
综上可得：函数f（x）-4在x∈R上的零点个数为3个，
故选：B．
当2＜x≤5时，y=2x-3；
当x＞5时，y=
| 1 |
| x |
∴y关于x的函数解析式为y=
|
∴当x≤2时，令f（x）-4=x2-4=0，可解得x=2或x=-2；
当2＜x≤5时，令f（x）-4=2x-3-4=0，可解得x=3.5；
当x＞5时，令f（x）-4=
| 1 |
| x |
综上可得：函数f（x）-4在x∈R上的零点个数为3个，
故选：B．
点评：本题主要考查了算法和程序框图，函数的性质及应用，属于基本知识的考查．
练习册系列答案
相关题目
双曲线上右支上存在点P，使得右焦点F关于直线OP的对称点在y轴上（O为坐标原点），则双曲线离心率的取值范围为（ ）
A、(
| ||||
B、(
| ||||
C、(1，
| ||||
D、(
|
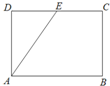
如图，在矩形ABCD中，AB=2，BC=
，E是CD的中点，那么
•
=（ ）
| 3 |
| AE |
| DC |
| A、4 | ||
| B、2 | ||
C、
| ||
| D、1 |
设命题p：?平面向量
和
，|
-
|＜|
|+|
|，则?p为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、?平面向量
| ||||||||||||
B、?平面向量
| ||||||||||||
C、?平面向量
| ||||||||||||
D、?平面向量
|