题目内容
有一个几何体的三视图及其尺寸如图所示,则该几何体的表面积和体积分别为( ) 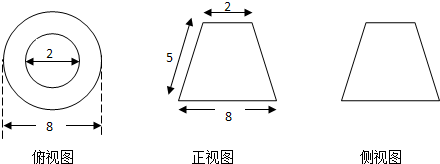

| A、42π,28π |
| B、28π,42π |
| C、24π,28π |
| D、82π,24π |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知:该几何体是圆台.ABCD为轴截面,其中AB=2,CD=8,AD=BC=5.分别过点A,B作AE⊥CD,BF⊥CD,垂足是E,F.可得DE=FC=
=3,在Rt△ADE中,AE=
=4.即可得出.
| 8-2 |
| 2 |
| AD2-DE2 |
解答:
解:由三视图可知:该几何体是圆台.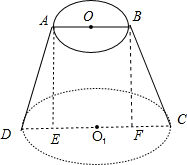
ABCD为轴截面,其中AB=2,CD=8,AD=BC=5.
分别过点A,B作AE⊥CD,BF⊥CD,垂足是E,F.
则DE=FC=
=3,
在Rt△ADE中,AE=
=4.
∴圆台的体积V=
(π×12+π×42+
)×4=28π.
表面积S=
(2π×1+2π×4)×5+π×42+π×12=42π.
故选:A.

ABCD为轴截面,其中AB=2,CD=8,AD=BC=5.
分别过点A,B作AE⊥CD,BF⊥CD,垂足是E,F.
则DE=FC=
| 8-2 |
| 2 |
在Rt△ADE中,AE=
| AD2-DE2 |
∴圆台的体积V=
| 1 |
| 3 |
| π×12×π×42 |
表面积S=
| 1 |
| 2 |
故选:A.
点评:本题考查了圆台的三视图、表面积与体积的计算公式,考查了计算能力,属于基础题.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
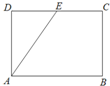
如图,在矩形ABCD中,AB=2,BC=
,E是CD的中点,那么
•
=( )
| 3 |
| AE |
| DC |

| A、4 | ||
| B、2 | ||
C、
| ||
| D、1 |
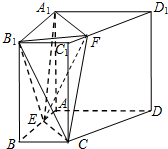 如图,在四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,∠BAD=90°,AD∥BC,且A1A=AB=AD=2BC=2,点E在棱AB上,平面A1EC与棱C1D1相交于点F.
如图,在四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,∠BAD=90°,AD∥BC,且A1A=AB=AD=2BC=2,点E在棱AB上,平面A1EC与棱C1D1相交于点F. 对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如表:
对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如表: