题目内容
10.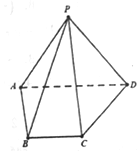 如图,三四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.
如图,三四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.(1)求异面直线PB与CD所成角的余弦值;
(2)线段AD上是否存在Q,使得它到平面PCD的距离为$\frac{3}{2}$?若存在,求出$\frac{AQ}{QD}$的值;若不存在,请说明理由.
分析 (1)取AD中点O,连接PO,BO,证明OBCD是平行四边形,可得OB∥DC,在证明PO⊥平面ABCD,∠POB是异面直线PB与CD所成的角,利用Rt△POA即可求解.
(2)假设存在点Q,使得它到平面的距离为$\frac{{\sqrt{3}}}{2}$.设QD=x,则${S_{△DQC}}=\frac{1}{2}x$,利用VP-DQC=VQ-PCD
求解x的值,即可得到$\frac{AQ}{QD}$的值.
解答 解:(1)设O为AD中点,连接PO,BO,在直角梯形ABCD中,BC∥AD,AD=2AB=2BC,
有OD∥BC且OD=BC,
∴四边形OBCD是平行四边形,所以OB∥DC,
在△PAD中PA=PD,O为AD中点,
∴PO⊥AD.侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,PO?平面PAD,∴PO⊥平面ABCD,
故PO⊥OB,∠POB为锐角,所以∠POB是异面直线PB与CD所成的角.
∵AD=2AB=2BC=2,在RtAOB中,AB=1,AO=1,
∴$OB=\sqrt{2}$,
在Rt△POA中,∵$AP=\sqrt{2},AO=1$,∴OP=1,
在Rt△PBO中,$PB=\sqrt{3}$,所以$cos∠PBO=\frac{{\sqrt{6}}}{3}$,
∴异面直线PB与CD所成的角的余弦值为$\frac{{\sqrt{6}}}{3}$.
(2)假设存在点Q,使得它到平面的距离为$\frac{{\sqrt{3}}}{2}$.
设QD=x,则${S_{△DQC}}=\frac{1}{2}x$,由(1)得$CD=OB=\sqrt{2}$,
在Rt△POC中,$PC=\sqrt{2}$,
∴$PC=CD=DP,{S_{△PCD}}=\frac{{\sqrt{3}}}{4}×{({\sqrt{2}})^2}=\frac{{\sqrt{3}}}{2}$,
由VP-DQC=VQ-PCD
解得:$x=\frac{3}{2}$,
∴存在点Q满足题意,
此时$\frac{AQ}{QD}=\frac{1}{3}$.
点评 本题主要考查了异面直线所成角的证明与计算,同时考查了体积关系的换算来求解距离问题.属于中档题.

| A. | b>a>c | B. | a>b>c | C. | c>b>a | D. | 无法确定 |
| A. | ($\frac{5}{12}$,$\frac{3}{4}$] | B. | ($\frac{5}{12}$,$\frac{3}{4}$) | C. | ($\frac{1}{3}$,$\frac{3}{4}$] | D. | (0,$\frac{5}{12}$) |
| A. | $\frac{19}{2}$ | B. | $\frac{21}{2}$ | C. | $\frac{21}{55}$ | D. | $\frac{23}{66}$ |
