题目内容
18.若过点p(1,$\sqrt{3}$)作圆O:x2+y2=1的两条切线,切点分别为A、B两点,则|AB|=$\sqrt{3}$.分析 根据题意画出相应的图形,由圆的方程找出圆心坐标和半径r,确定出|OA|与|OB|的长,由切线的性质得到OA与AP垂直,OB与PB垂直,且切线长相等,由P与O的坐标,利用两点间的距离公式求出|OP|的长,在直角三角形AOP中,利用勾股定理求出|AP|的长,同时得到∠APO=30°,确定出三角形APB为等边三角形,由等边三角形的边长相等得到|AB|=|OP|,可得出|AB|的长.
解答  解:由圆的方程x2+y2=1,得到圆心O(0,0),半径r=1,
解:由圆的方程x2+y2=1,得到圆心O(0,0),半径r=1,
∴|OA|=|OB|=1,
∵PA、PB分别为圆的切线,
∴OA⊥AP,OB⊥PB,|PA|=|PB|,OP为∠APB的平分线,
∵P(1,$\sqrt{3}$),O(0,0),
∴|OP|=2,
在Rt△AOP中,根据勾股定理得:|AP|=$\sqrt{4-1}$=$\sqrt{3}$,
∵|OA|=$\frac{1}{2}$|OP|,∴∠APO=30°,
∴∠APB=60°,
∴△PAB为等边三角形,
则|AB|=|AP|=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 此题考查了直线与圆的位置关系,直线与圆的位置关系由d与r的大小关系确定,当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交(d表示圆心到直线的距离,r表示圆的半径).

练习册系列答案
相关题目
13.我国古代数学名著《九章算术》中,有已知长方形面积求一边的算法,其方法的前两步为:
第一步:构造数列1,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,…,$\frac{1}{n}$.①
第二步:将数列①的各项乘以n,得到数列(记为)a1,a2,a3,…,an.则a1a2+a2a3+…+an-1an=( )
第一步:构造数列1,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,…,$\frac{1}{n}$.①
第二步:将数列①的各项乘以n,得到数列(记为)a1,a2,a3,…,an.则a1a2+a2a3+…+an-1an=( )
| A. | n2 | B. | (n-1)2 | C. | n(n-1) | D. | n(n+1) |
3.已知映射f:A→B,其中A={x|x>0},B=R,对应法则f:x→-x2+2x,对于实数k∈B,在集合A中存在两个不同的原像,则k的取值范围为( )
| A. | k>0 | B. | k<1 | C. | 0<k≤1 | D. | 0<k<1 |
8.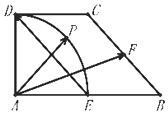 在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为
在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为
AB,AC 的中点,以A 为圆心,AD为半径的圆弧DE中点为P (如图所示).
若$\overrightarrow{AP}=λ\overrightarrow{ED}+μ\overrightarrow{AF}$,其中λ,μ∈R,则λ+μ的值是( )
 在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为
在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为AB,AC 的中点,以A 为圆心,AD为半径的圆弧DE中点为P (如图所示).
若$\overrightarrow{AP}=λ\overrightarrow{ED}+μ\overrightarrow{AF}$,其中λ,μ∈R,则λ+μ的值是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{3\sqrt{2}}}{4}$ | C. | $\sqrt{2}$ | D. | $\frac{3}{4}$ |

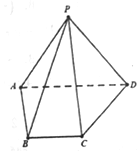 如图,三四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.
如图,三四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.