题目内容
5.曲线y=1+$\sqrt{4-{x}^{2}}$与直线kx-y-2k+4=0有两个交点时,实数k取值范围是( )| A. | ($\frac{5}{12}$,$\frac{3}{4}$] | B. | ($\frac{5}{12}$,$\frac{3}{4}$) | C. | ($\frac{1}{3}$,$\frac{3}{4}$] | D. | (0,$\frac{5}{12}$) |
分析 先将曲线进行化简得到一个圆心是(0,1)的上半圆,直线y=k(x-2)+4表示过定点(2,4)的直线,利用直线与圆的位置关系可以求实数k的取值范围.
解答 解:因为曲线y=1+$\sqrt{4-{x}^{2}}$所以x2+(y-1)2=4,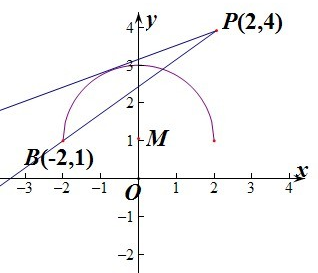
此时表示为圆心M(0,1),半径r=2的圆.
因为x∈[-2,2],y=1+$\sqrt{4-{x}^{2}}$≥1,
所以表示为圆的上部分.
直线y=k(x-2)+4表示过定点P(2,4)的直线,
当直线与圆相切时,有圆心到直线kx-y+4-2k=0的距离d=$\frac{|3-2k|}{\sqrt{{k}^{2}+1}}$=2,解得k=$\frac{5}{12}$.
当直线经过点B(-2,1)时,直线PB的斜率为k=$\frac{3}{4}$.
所以要使直线与曲线有两个不同的公共点,则必有$\frac{5}{12}$<k≤$\frac{3}{4}$.
即实数k的取值范围是$\frac{5}{12}$<k≤$\frac{3}{4}$.
故选A.
点评 本题主要考查了直线与圆的位置关系的应用以及直线的斜率和距离公式.利用数形结合思想是解决本题的关键.同时要注意曲线化简之后是个半圆,而不是整圆,这点要注意,防止出错.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
15.在△ABC中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}=\overrightarrow b$,P在边BC上且BP=2PC,则$\overrightarrow{AP}$=( )
| A. | $\frac{4}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | B. | $\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | C. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | D. | $\frac{1}{3}\overrightarrow a+\frac{4}{3}\overrightarrow b$ |
16.设函数f(x)=sin(2x+$\frac{π}{3}$),则下列关于函数f(x)的说法中正确的是( )
| A. | f(x)是偶函数 | B. | f(x)最小正周期为2π | ||
| C. | f(x)图线关于直线点x=-$\frac{π}{6}$对称 | D. | f(x)图象关于点(-$\frac{π}{6}$,0)对称 |
13.我国古代数学名著《九章算术》中,有已知长方形面积求一边的算法,其方法的前两步为:
第一步:构造数列1,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,…,$\frac{1}{n}$.①
第二步:将数列①的各项乘以n,得到数列(记为)a1,a2,a3,…,an.则a1a2+a2a3+…+an-1an=( )
第一步:构造数列1,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,…,$\frac{1}{n}$.①
第二步:将数列①的各项乘以n,得到数列(记为)a1,a2,a3,…,an.则a1a2+a2a3+…+an-1an=( )
| A. | n2 | B. | (n-1)2 | C. | n(n-1) | D. | n(n+1) |
17.已知函数$f(n)=\left\{\begin{array}{l}{n^2}(当n为奇数时)\\-{n^2}(当n为偶数时)\end{array}\right.$且an=f(n)+f(n+1),则a1+a2+…+a99等于( )
| A. | 0 | B. | 100 | C. | -101 | D. | -99 |
14.已知全集U={1,2,3,4,5},集合A={3,4},B={1,2},则(∁UA)∩B等于( )
| A. | {1,2} | B. | [1,3} | C. | {1,2,5} | D. | {1,2,3} |
15.已知集合A={1,3,5},B={1,m},A∩B={1,m},则m等于( )
| A. | 1 或 3 | B. | 3 或 5 | C. | 1 或 5 | D. | 1 或 3 或5 |
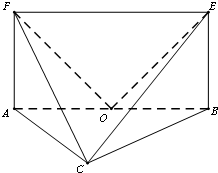 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.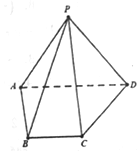 如图,三四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.
如图,三四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.