题目内容
15.数列{an}满足a1=2,a2=1,并且$\frac{1}{{{a_{n-1}}}}=\frac{2}{a_n}-\frac{1}{{{a_{n+1}}}}(n≥2)$.则a10+a11=( )| A. | $\frac{19}{2}$ | B. | $\frac{21}{2}$ | C. | $\frac{21}{55}$ | D. | $\frac{23}{66}$ |
分析 由已知数列递推式可知数列{$\frac{1}{{a}_{n}}$}为等差数列,求出等差数列的通项公式,得到an,则答案可求.
解答 解:由$\frac{1}{{{a_{n-1}}}}=\frac{2}{a_n}-\frac{1}{{{a_{n+1}}}}(n≥2)$,得$\frac{1}{{a}_{n-1}}+\frac{1}{{a}_{n+1}}=\frac{2}{{a}_{n}}$,
∴数列{$\frac{1}{{a}_{n}}$}为等差数列,
又a1=2,a2=1,
∴数列{$\frac{1}{{a}_{n}}$}的公差为d=$\frac{1}{{a}_{2}}-\frac{1}{{a}_{1}}=1-\frac{1}{2}=\frac{1}{2}$,
则$\frac{1}{{a}_{n}}=\frac{1}{2}+\frac{1}{2}(n-1)=\frac{n}{2}$,
∴${a}_{n}=\frac{2}{n}$.
则a10+a11=$\frac{2}{10}+\frac{2}{11}=\frac{21}{55}$.
故选:C.
点评 本题考查数列递推式,考查了等差关系的确定,训练了等差数列通项公式的求法,是中档题.

练习册系列答案
相关题目
3.已知映射f:A→B,其中A={x|x>0},B=R,对应法则f:x→-x2+2x,对于实数k∈B,在集合A中存在两个不同的原像,则k的取值范围为( )
| A. | k>0 | B. | k<1 | C. | 0<k≤1 | D. | 0<k<1 |
20.在△ABC中,角A、B、C所对的边分别为a、b、c,已知$b=2,A=\frac{π}{3}$,且$\frac{c}{1-cosC}=\frac{b}{cosA}$,则△ABC的面积为( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$或$\sqrt{3}$ | D. | $\sqrt{3}$或$2\sqrt{3}$ |

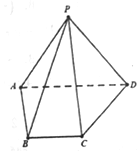 如图,三四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.
如图,三四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.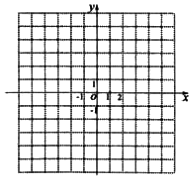 已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4x,x≥0}\\{{a}^{x}-1,x<0}\end{array}\right.$,(x>0且a≠1)的图象经过点(-2,3).
已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4x,x≥0}\\{{a}^{x}-1,x<0}\end{array}\right.$,(x>0且a≠1)的图象经过点(-2,3).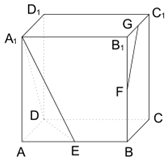 如 图,正方体ABCD-A1B1C1D1的棱长为2,E、F、G 分别为 AB、BB1、B1C1 的中点.
如 图,正方体ABCD-A1B1C1D1的棱长为2,E、F、G 分别为 AB、BB1、B1C1 的中点.