题目内容
2.已知△ABC中,$a=2\sqrt{3},b=2,B=30°$,则角A=60°,或120°.分析 由已知及正弦定理可求sinA=$\frac{asinB}{b}$=$\frac{\sqrt{3}}{2}$,结合a>b,A为三角形内角,可求范围A∈(30°,180°),即可得解A的值.
解答 解:∵$a=2\sqrt{3},b=2,B=30°$,
∴由正弦定理可得:sinA=$\frac{asinB}{b}$=$\frac{2\sqrt{3}×sin30°}{2}$=$\frac{\sqrt{3}}{2}$,
又∵a>b,A为三角形内角,即A∈(30°,180°),
∴A=60°,或120°.
故答案为:60°,或120°.
点评 本题主要考查了正弦定理,大边对大角,特殊角的三角函数值在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
12.设a>b>1,c<0,给出下列四个结论:
①ac>1;②ac<bc;③logb(a-c)>logb(b-c);④ab-c>aa-c,
其中所有的正确结论的序号是( )
①ac>1;②ac<bc;③logb(a-c)>logb(b-c);④ab-c>aa-c,
其中所有的正确结论的序号是( )
| A. | ①② | B. | ②③ | C. | ①②③ | D. | ②③④ |
13.我国古代数学名著《九章算术》中,有已知长方形面积求一边的算法,其方法的前两步为:
第一步:构造数列1,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,…,$\frac{1}{n}$.①
第二步:将数列①的各项乘以n,得到数列(记为)a1,a2,a3,…,an.则a1a2+a2a3+…+an-1an=( )
第一步:构造数列1,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,…,$\frac{1}{n}$.①
第二步:将数列①的各项乘以n,得到数列(记为)a1,a2,a3,…,an.则a1a2+a2a3+…+an-1an=( )
| A. | n2 | B. | (n-1)2 | C. | n(n-1) | D. | n(n+1) |
17.已知函数$f(n)=\left\{\begin{array}{l}{n^2}(当n为奇数时)\\-{n^2}(当n为偶数时)\end{array}\right.$且an=f(n)+f(n+1),则a1+a2+…+a99等于( )
| A. | 0 | B. | 100 | C. | -101 | D. | -99 |
14.已知全集U={1,2,3,4,5},集合A={3,4},B={1,2},则(∁UA)∩B等于( )
| A. | {1,2} | B. | [1,3} | C. | {1,2,5} | D. | {1,2,3} |
11.经过点A(-1,4)且在x轴上的截距为3的直线方程是( )
| A. | x+y+3=0 | B. | x-y+5=0 | C. | x+y-3=0 | D. | x+y-5=0 |
12.在空间直角坐标系Oxyz中,z轴上的点M到点A(1,0,2)与点B(1,-3,1)的距离相等,则点M的坐标是( )
| A. | (0,0,-3) | B. | (0,0,3) | C. | (0,0,$\sqrt{10}$) | D. | (0,0,-$\sqrt{10}$) |
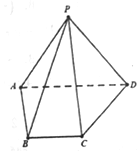 如图,三四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.
如图,三四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.