题目内容
求下列各三角函数式的值.
(1)2cos300°+sin630°
(2)已知tanα=
,求
的值.
(1)2cos300°+sin630°
(2)已知tanα=
| 1 |
| 2 |
| 2cosα-3sinα |
| 3cosα+4sinα |
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)原式中的角度变形后,利用诱导公式及特殊角的三角函数值计算即可得到结果;
(2)原式分子分母除以cosα,利用同角三角函数间基本关系弦化切后,将tanα的值代入计算即可求出值.
(2)原式分子分母除以cosα,利用同角三角函数间基本关系弦化切后,将tanα的值代入计算即可求出值.
解答:
解:(1)原式=2cos(360°-60°)+sin(720°-90°)=2cos60°-sin90°=1-1=0;
(2)∵tanα=
,
∴原式=
=
=
.
(2)∵tanα=
| 1 |
| 2 |
∴原式=
| 2-3tanα |
| 3+4tanα |
2-3×
| ||
3+4×
|
| 1 |
| 10 |
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
已知a>b>0,c∈R,则下列不等式恒成立的是( )
| A、ac>bc | ||||
| B、c-a>c-b | ||||
| C、a2<b2 | ||||
D、
|
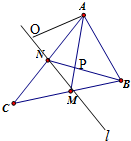 在△ABC中,已知AB=2,AC=6,∠BAC=60°,中线AM、BN交于点P,设
在△ABC中,已知AB=2,AC=6,∠BAC=60°,中线AM、BN交于点P,设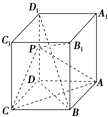 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.求证:
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.求证: