题目内容
已知f(x)=aln(x+1)+
+3x-1.
(1)若x≥0时,f(x)≥0恒成立,求实数a的取值范围;
(2)求证:
+
+
+…+
>
ln(2n+1)对一切正整数n均成立.
| 1 |
| x+1 |
(1)若x≥0时,f(x)≥0恒成立,求实数a的取值范围;
(2)求证:
| 2 |
| 4×12-1 |
| 3 |
| 4×22-1 |
| 4 |
| 4×32-1 |
| n+1 |
| 4×n2-1 |
| 1 |
| 4 |
考点:不等式的证明
专题:选作题,不等式
分析:(1)求导数,分类讨论,确定函数的单调性,即可求实数a的取值范围;
(2)由(1)知,x>0时,不等式-2ln(x+1)+
+3x-1>0恒成立,则x>0时,
+3x-1>2ln(x+1)恒成立.令x=
(k∈N*),
>
ln
.令k=1,2,3,…,n,叠加,即可证明结论.
(2)由(1)知,x>0时,不等式-2ln(x+1)+
| 1 |
| x+1 |
| 1 |
| x+1 |
| 2 |
| 2k-1 |
| k+1 |
| 4k2-1 |
| 1 |
| 4 |
| 2k+1 |
| 2k-1 |
解答:
(1)解:f′(x)=
-
+3=
=
.
若a≥-2,则a+6>0,x>0时,f'(x)>0.此时,f(x)在区间[0,+∞)上为增函数.
∴x≥0时,f(x)≥f(0)=0.a≥-2符合要求.
若a<-2,则方程3x2+(a+6)x+a+2=0有两个异号的实根,设这两个实根为x1,x2,且x1<0<x2.
∴0<x<x2时,f'(x)<0.f(x)在区间[0,x2]上为减函数,f(x2)<f(0)=0.
∴a<-2不符合要求.
∴a的取值范围为[-2,+∞).
(2)证明:由(1)知,x>0时,不等式-2ln(x+1)+
+3x-1>0恒成立.
∴x>0时,
+3x-1>2ln(x+1)恒成立.
令x=
(k∈N*),得
+3×
-1>2ln(
+1),
整理得
>2ln
.
∴
>
ln
.令k=1,2,3,…,n,得
>
ln
,
>
ln
,
>
ln
,…,
>
ln
.
将上述n个不等式的左右两边分别相加,得
+
+
+…+
>
ln(
×
×
×…×
)=
ln(2n+1).
∴
+
+
+…+
>
ln(2n+1)对一切正整数n均成立.
| a |
| x+1 |
| 1 |
| (x+1)2 |
| 3(x+1)2+a(x+1)-1 |
| (x+1)2 |
| 3x2+(a+6)x+a+2 |
| (x+1)2 |
若a≥-2,则a+6>0,x>0时,f'(x)>0.此时,f(x)在区间[0,+∞)上为增函数.
∴x≥0时,f(x)≥f(0)=0.a≥-2符合要求.
若a<-2,则方程3x2+(a+6)x+a+2=0有两个异号的实根,设这两个实根为x1,x2,且x1<0<x2.
∴0<x<x2时,f'(x)<0.f(x)在区间[0,x2]上为减函数,f(x2)<f(0)=0.
∴a<-2不符合要求.
∴a的取值范围为[-2,+∞).
(2)证明:由(1)知,x>0时,不等式-2ln(x+1)+
| 1 |
| x+1 |
∴x>0时,
| 1 |
| x+1 |
令x=
| 2 |
| 2k-1 |
| 1 | ||
|
| 2 |
| 2k-1 |
| 2 |
| 2k-1 |
整理得
| 8k+8 |
| 4k2-1 |
| 2k+1 |
| 2k-1 |
∴
| k+1 |
| 4k2-1 |
| 1 |
| 4 |
| 2k+1 |
| 2k-1 |
| 2 |
| 4×12-1 |
| 1 |
| 4 |
| 3 |
| 1 |
| 3 |
| 4×22-1 |
| 1 |
| 4 |
| 5 |
| 3 |
| 4 |
| 4×32-1 |
| 1 |
| 4 |
| 7 |
| 5 |
| n+1 |
| 4×n2-1 |
| 1 |
| 4 |
| 2n+1 |
| 2n-1 |
将上述n个不等式的左右两边分别相加,得
| 2 |
| 4×12-1 |
| 3 |
| 4×22-1 |
| 4 |
| 4×32-1 |
| n+1 |
| 4×n2-1 |
| 1 |
| 4 |
| 3 |
| 1 |
| 5 |
| 3 |
| 7 |
| 5 |
| 2n+1 |
| 2n-1 |
| 1 |
| 4 |
∴
| 2 |
| 4×12-1 |
| 3 |
| 4×22-1 |
| 4 |
| 4×32-1 |
| n+1 |
| 4×n2-1 |
| 1 |
| 4 |
点评:本题考查导数知识的运用,考查函数的单调性,考查不等式的证明,巧妙利用两小题之间的关系,是解题的关键.

练习册系列答案
相关题目
已知点A(1,3),B(4,-1),则与向量
方向相反的单位向量为( )
| AB |
A、(
| ||||
B、(-
| ||||
C、(
| ||||
D、(-
|
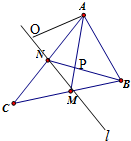 在△ABC中,已知AB=2,AC=6,∠BAC=60°,中线AM、BN交于点P,设
在△ABC中,已知AB=2,AC=6,∠BAC=60°,中线AM、BN交于点P,设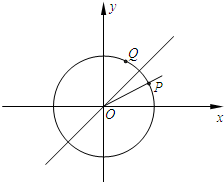 如图,已知单位圆上两点P,Q关于直线y=x对称,且以x轴正半轴为始边、以射线OP为终边的角的大小为x.
如图,已知单位圆上两点P,Q关于直线y=x对称,且以x轴正半轴为始边、以射线OP为终边的角的大小为x.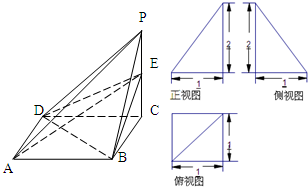 已知四棱锥P-ABCD的三视图和直观图如图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E是侧棱PC上的动点.
已知四棱锥P-ABCD的三视图和直观图如图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E是侧棱PC上的动点.