题目内容
11.下列判断错误的是( )| A. | 命题“若am2≤bm2,则a≤b”是假命题 | |
| B. | 直线y=$\frac{1}{2}$x+b不能作为函数f(x)=$\frac{1}{{e}^{x}}$图象的切线 | |
| C. | “若a=1,则直线x+y=0和直线x-ay=0互相垂直”的逆否命题为真命题 | |
| D. | “f′(x0)=0”是“函数f(x)在x0处取得极值”的充分不必要条件 |
分析 分别判断A,B,C,D中四个答案的正误,综合分析结果,可得结论.
解答 解:命题“若am2≤bm2,则a≤b”当m=0时不成立,故是假命题,故A正确;
f′(x)=-$\frac{1}{{e}^{x}}$<0恒成立,故函数f(x)=$\frac{1}{{e}^{x}}$图象的切线斜率恒为负,故直线y=$\frac{1}{2}$x+b不能作为函数f(x)=$\frac{1}{{e}^{x}}$图象的切线,故B正确;
“若a=1,则直线x+y=0和直线x-ay=0互相垂直”为真命题,故其逆否命题也为真命题,故C正确;
“f′(x0)=0”是“函数f(x)在x0处取得极值”的必要不充分条件,故D错误;
故选:D
点评 本题以命题的真假判断与应用为载体,考查了不等式的基本性质,导数的几何意义,直线垂直,四种命题,充要条件,难度中档.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.已知等差数列{an}满足a2=2,点(a4,a6)在直线x+2y-16=0上.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Sn.
19.判断两个变量y与x是否相关时,选择了4个不同的模型,它们的相关指数R2分别为:模型1的相关指数R2为0.86,模型2的相关指数R2为0.68,模型3的相关指数R2为0.88,模型4的相关指数R2为0.66.其中拟合效果最好的模型是( )
| A. | 模型1 | B. | 模型2 | C. | 模型3 | D. | 模型4 |
1.下列各式错误的是( )
| A. | 30.8>30.7 | B. | log0.50.4>log0.50.6 | ||
| C. | 0.75-0.1<0.750.1 | D. | log2$\sqrt{3}$>log3$\sqrt{2}$ |
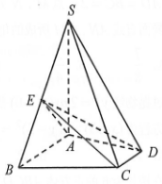 如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD=2,E是边SB的中点.
如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD=2,E是边SB的中点.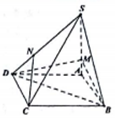 如图,四棱锥S-ABCD中,底面ABCD是边长为4的菱形,∠ABC=60°,SA⊥平面ABCD,且SA=4,M在棱SA上,且AM=1,N在棱SD上且SN=2ND.
如图,四棱锥S-ABCD中,底面ABCD是边长为4的菱形,∠ABC=60°,SA⊥平面ABCD,且SA=4,M在棱SA上,且AM=1,N在棱SD上且SN=2ND.