题目内容
1.已知等差数列{an}满足a2=2,点(a4,a6)在直线x+2y-16=0上.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Sn.
分析 (I)设等差数列{an}的公差为d,由点(a4,a6)在直线x+2y-16=0上,可得a4+2a6-16=0,又a2=2,即∴3a1+13d-16=0,a1+d=2,解得a1,d,即可得出.
(II)bn=an+2${\;}^{{a}_{n}}$=n+2n.利用等差数列与等比数列的求和公式即可得出.
解答 解:(I)设等差数列{an}的公差为d,
∵点(a4,a6)在直线x+2y-16=0上,∴a4+2a6-16=0,又a2=2,
∴3a1+13d-16=0,a1+d=2,解得a1=d=1,
∴an=1+(n-1)=n.
(II)bn=an+2${\;}^{{a}_{n}}$=n+2n.
∴数列{bn}的前n项和Sn=$\frac{n(n+1)}{2}$+$\frac{2({2}^{n}-1)}{2-1}$=$\frac{n(n+1)}{2}$+2n+1-2.
点评 本题考查了等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
11.阅读如图的程序框图,运行相应的程序,则输出的值为( )
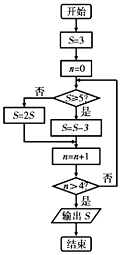

| A. | 3 | B. | 4 | C. | 6 | D. | 7 |
12.已知f(x)=$\left\{\begin{array}{l}{e^x}+a{x^2},x>0\\ \frac{1}{e^x}+a{x^2},x<0\end{array}$,若函数f(x)有四个零点,则实数a的取值范围是( )
| A. | (-∞,-e) | B. | (-∞,-$\frac{{e}^{2}}{4}$) | C. | (-∞,-$\frac{{e}^{3}}{9}$) | D. | (-∞,-$\frac{{e}^{4}}{16}$) |
9.已知函数f(x)=ex+$\frac{2x-5}{{x}^{2}+1}$的图象在点(0,f(0))处的切线与直线x-my+4=0垂直,则实数m的值为( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
16.已知函数f(x)=lgx,0<a<b,若p=f($\sqrt{ab}$),q=f($\frac{a+b}{2}$),r=$\frac{1}{2}$[f(a)+f(b)],则p,q,r的大小关系是( )
| A. | p=r>q | B. | p=r<q | C. | q=r<p | D. | q-r>p |
6.若直线2x+y-4=0,x+ky-3=0与两坐标轴围成的四边形有外接圆,则此四边形的面积为( )
| A. | $\frac{11}{4}$ | B. | $\frac{5\sqrt{5}}{4}$ | C. | $\frac{41}{20}$ | D. | 5 |
11.下列判断错误的是( )
| A. | 命题“若am2≤bm2,则a≤b”是假命题 | |
| B. | 直线y=$\frac{1}{2}$x+b不能作为函数f(x)=$\frac{1}{{e}^{x}}$图象的切线 | |
| C. | “若a=1,则直线x+y=0和直线x-ay=0互相垂直”的逆否命题为真命题 | |
| D. | “f′(x0)=0”是“函数f(x)在x0处取得极值”的充分不必要条件 |