题目内容
16．
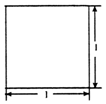若一个底面是等腰直角三角形的直三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为（ ）| A． | 6π或5π | B． | 3π或5π | C． | 6π | D． | 5π |
分析 由题意，根据几何体的放置位置不同，得到三视图的正视图不同；本题的正视图可能是底面三角形的一腰与高组成的正视图，也可能是等腰三角形的斜边高组成的正视图；因此由两种可能计算表面积．
解答 解：①当此正视图是底面三角形的一腰与高组成，此时三棱柱对应的正方体长宽高分别是1，1，1，其体对角线长度为$\sqrt{3}$，所以外接球表面积为$4π（\frac{\sqrt{3}}{2}）^{2}=3π$；
②当正视图是等腰三角形的斜边高与棱柱的高组成的，此时三棱柱对应的长方体长宽高分别是$\sqrt{2}$，$\sqrt{2}$，1，所以体对角线长度为$\sqrt{5}$，所以其外接球的表面积为$4π（\frac{\sqrt{5}}{2}）^{2}=5π$；
故选B．
点评 本题考查了几何体的三视图；关键是明确正视图的形成过程，明确外接球的直径与几何体的关系．
练习册系列答案
名校课堂系列答案
相关题目
19．已知p：a＞|b|，q：a2＞b2，则下列结论正确的是（ ）
| A． | p是q的充分不必要条件 | B． | p是q的必要不充分条件 | ||
| C． | p是q的既不充分也不必要条件 | D． | p是q的充要条件 |
7．已知函数f（x）=x2+ax+b，m，n满足m＜n且f（m）=n，f（n）=m，则当m＜x＜n时，（ ）
| A． | f（x）+x＜m+n | B． | f（x）+x＞m+n | C． | f（x）-x＜0 | D． | f（x）-x＞0 |
11．已知函数f（x）=4ex（x+1）-k（$\frac{2}{3}$x3+2x2），若x=-2是函数f（x）的唯一一个极值点，则实数k的取值范围是（ ）
| A． | （-2e，e] | B． | [0，2e] | C． | （-∞，-e）∪[e，2e] | D． | （-∞，-e）∪[0，e] |
1．调查者通过询问64名男女大学生在购买食品时是否看营养说明，得到的数据如表所示：
问大学生的性别与是否看营养说明之间有没有关系？
附：参考公式与数据：χ2=$\frac{{n{{（n}_{11}n}_{22}{{-n}_{12}n}_{21}）}^{2}}{{n}_{1}{+n}_{2}{{+n}_{+1}n}_{+2}}$．当χ2＞3.841时，有95%的把握说事件A与B有关；当χ2＞6.635时，有99%的把握说事件A与B有关；当χ2≤3.841时，有95%的把握说事件A与B是无关的．
| 看营养说明 | 不看营养说明 | 合计 | |
| 男大学生 | 26 | 6 | 32 |
| 女大学生 | 14 | 18 | 32 |
| 合计 | 40 | 24 | 64 |
附：参考公式与数据：χ2=$\frac{{n{{（n}_{11}n}_{22}{{-n}_{12}n}_{21}）}^{2}}{{n}_{1}{+n}_{2}{{+n}_{+1}n}_{+2}}$．当χ2＞3.841时，有95%的把握说事件A与B有关；当χ2＞6.635时，有99%的把握说事件A与B有关；当χ2≤3.841时，有95%的把握说事件A与B是无关的．