题目内容

7．已知函数f（x）=x2+ax+b，m，n满足m＜n且f（m）=n，f（n）=m，则当m＜x＜n时，（　　）
A．f（x）+x＜m+nB．f（x）+x＞m+nC．f（x）-x＜0D．f（x）-x＞0

分析 设A（m，n），B（n，m），求出直线AB的方程，根据f（x）的开口方向即可得出f（x）与直线y=-x+m+n的大小关系，从而得出答案．

解答 解：设A（m，n），B（n，m），则直线AB的方程为y=-x+m+n，
即A，B为直线y=-x+m+n与f（x）的图象的两个交点，
∵f（x）的图象开口向上，
∴当m＜x＜n时，f（x）＜-x+m+n，即f（x）+x＜m+n，
故选A．

点评 本题考查了二次函数的性质，不等式的解与函数图象的关系，属于中档题．

练习册系列答案
相关题目
10．已知$|{\overrightarrow a}|=4$，$|{\overrightarrow b}|=\sqrt{2}$，$\overrightarrow a$与$\overrightarrow b$夹角为135°，则$\overrightarrow a•（\overrightarrow a+\vec b）$=12．
11．已知函数f（x）=ax2-a-lnx．
（Ⅰ）试讨论f（x）的单调性；
（Ⅱ）若f（x）+$\frac{e}{{e}^{x}}$-$\frac{1}{x}$＞0在（1，+∞）上恒成立，求实数a的取值范围．
8．若样本平均数为$\overline{x}$，总体平均数为μ，则（　　）
A．$\overline{x}$=μB．$\overline{x}$≈μC．μ是$\overline{x}$的估计值D．$\overline{x}$是μ的估计值
2．若函数f（x）=4x+a•2x+a+1在R上存在零点，则实数a的取值范围为（-∞，2-2$\sqrt{2}$]．
12．已知F1，F2是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左，右焦点，离心率为$\frac{1}{2}$，M、N是平面内两点，满足$\overrightarrow{{F}_{1}M}$=-2$\overrightarrow{M{F}_{2}}$，线段NF1的中点P在椭圆上，△F1MN周长为12
（1）求椭圆C的方程；
（2）若与圆x2+y2=1相切的直线l与椭圆C交于A、B，求$\overrightarrow{OA}$$•\overrightarrow{OB}$（其中O为坐标原点）的取值范围．
19．直线$\left\{\begin{array}{l}x=1+tcosα\\ y=-2+tsinα\end{array}$（t为参数，0≤a＜π）必过点（　　）
A．（1，-2）B．（-1，2）C．（-2，1）D．（2，-1）
16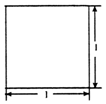．若一个底面是等腰直角三角形的直三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为（　　）
A．6π或5πB．3π或5πC．6πD．5π
17．已知等差数列{an}满足a2=3，a4+a7=20．
（Ⅰ）求数列{an}的通项an及前n项和为Sn；
（Ⅱ）在（Ⅰ）的条件下，证明：$\sum_{k=1}^{n}$$\frac{1}{{S}_{K}}$＜$\frac{5}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网