题目内容
已知某种同品牌的6瓶饮料中有2瓶已过了保质期.
(Ⅰ)从6瓶饮料中任意抽取1瓶,求抽到没过保质期的饮料的概率;
(Ⅱ)从6瓶饮料中任意抽取2瓶(不分先后顺序).
(i)写出所有可能的抽取结果;
(ii)求抽到已过保质期的饮料的概率.
(Ⅰ)从6瓶饮料中任意抽取1瓶,求抽到没过保质期的饮料的概率;
(Ⅱ)从6瓶饮料中任意抽取2瓶(不分先后顺序).
(i)写出所有可能的抽取结果;
(ii)求抽到已过保质期的饮料的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(I)从6瓶饮料中任意抽取1瓶的基本事件个数为
.从没过保质期的饮料中任意抽取1瓶的基本事件个数为
.从而得到从6瓶饮料中任意抽取1瓶,抽到没过保质期的饮料的概率.
(II)从6瓶饮料中任意抽取2瓶的基本事件个数为
.
(i)给六瓶饮料编号后,利用列举法,可得到所有可能的抽取结果;
(ii)列举出所有抽到已过保质期的饮料的抽取结果,代入古典概型概率计算公式,可得答案.
| C | 1 6 |
| C | 1 4 |
(II)从6瓶饮料中任意抽取2瓶的基本事件个数为
| C | 2 6 |
(i)给六瓶饮料编号后,利用列举法,可得到所有可能的抽取结果;
(ii)列举出所有抽到已过保质期的饮料的抽取结果,代入古典概型概率计算公式,可得答案.
解答:
解:(I)∵从6瓶饮料中任意抽取1瓶的基本事件个数为
=6,
从没过保质期的饮料中任意抽取1瓶的基本事件个数为
=4,
∴从6瓶饮料中任意抽取1瓶,抽到没过保质期的饮料的概率P=
=
.
(II)(i)记4瓶没有过保持期的饮料为a,b,c,d,2瓶已过保质期的饮料为A,B,
记从中抽取两瓶为(x,y),则共有:
(a,b),(a,c),(a,d),(a,A),(a,B),
(b,c),(b,d),(b,A),(b,B),(c,d),
(c,A),(c,B),(d,A),(d,B),(A,B)共15种不同情况;
(i)记“抽到已过保质期的饮料”为事件A,
则A中共包含:
(a,A),(a,B),(b,A),(b,B),(c,A),(c,B),(d,A),(d,B),(A,B)共9种不同情况;
故P(A)=
=
,
即抽到已过保质期的饮料的概率为
| C | 1 6 |
从没过保质期的饮料中任意抽取1瓶的基本事件个数为
| C | 1 4 |
∴从6瓶饮料中任意抽取1瓶,抽到没过保质期的饮料的概率P=
| 4 |
| 6 |
| 2 |
| 3 |
(II)(i)记4瓶没有过保持期的饮料为a,b,c,d,2瓶已过保质期的饮料为A,B,
记从中抽取两瓶为(x,y),则共有:
(a,b),(a,c),(a,d),(a,A),(a,B),
(b,c),(b,d),(b,A),(b,B),(c,d),
(c,A),(c,B),(d,A),(d,B),(A,B)共15种不同情况;
(i)记“抽到已过保质期的饮料”为事件A,
则A中共包含:
(a,A),(a,B),(b,A),(b,B),(c,A),(c,B),(d,A),(d,B),(A,B)共9种不同情况;
故P(A)=
| 9 |
| 15 |
| 3 |
| 5 |
即抽到已过保质期的饮料的概率为
| 3 |
| 5 |
点评:此题考查了古典概型概率计算公式,掌握古典概型概率公式:概率=所求情况数与总情况数之比是解题的关键.

练习册系列答案
相关题目
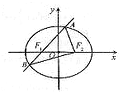 如图,椭圆E:
如图,椭圆E: