Question

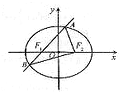如图，椭圆E：

x2

a2

+

y2

b2

=1（a＞b＞0）的左焦点为F₁，右焦点为F₂，离心率e=

1

2

．过F₁的直线l交椭圆与A、B两点，且△ABF₂的周长为8．
（1）求椭圆E的方程；
（2）当△ABF₂的面积为3时，求直线l的方程．

Answer 1

考点：直线与圆锥曲线的关系,椭圆的标准方程

专题：综合题,圆锥曲线的定义、性质与方程

分析：（1）由△ABF₂的周长为8，结合椭圆定义求得a值，再由椭圆离心率求出c，由b²=a²-c²求得b，则椭圆方程可求；
（2）设出直线l的方程为x=ty-1，和椭圆方程联立后化为关于y的一元二次方程，利用根与系数关系求出A，B两点纵坐标的和与积，由S△ABF2=

1

2

|F1F2|•|y1-y2|，整理后代入根与系数关系求得t值，则直线方程可求．

解答： 解：（1）∵|AB|+|AF₂|+|BF₂|=8，
即|AF₁|+|F₁B|+|AF₂|+|BF₂|=8，
又|AF₁|+|AF₂|=|BF₁|+|BF₂|=2a，
∴4a=8，a=2．
又∵e=

1

2

，即

c

a

=

1

2

，
∴c=1．
∴b=

a2-c2

=

3

．
故椭圆E的方程为

x2

4

+

y2

3

=1；
（2）设直线l的方程为x=ty-1．
联立

x=ty-1 x2 4 + y2 3 =1

，得（3t²+4）y²-6ty-9=0．
设A（x₁，y₁），B（x₂，y₂），
则y1+y2=

6t

3t2+4

，y1y2=

-9

3t2+4

．
由S△ABF2=

1

2

|F1F2|•|y1-y2|=

1

2

×2×

(y1+y2)2-4y1y2

=

( 6t 3t2+4 )2+4× 9 3t2+4

=

12

3t2+4

•

t2+1

=3，
解得：t=0．
∴直线l的方程为x=-1．

点评：本题主要考查椭圆的性质，直线与圆锥曲线的位置关系，考查运算求解能力，推理论证能力，考查化归与转化思想方法，函数与方程思想，是压轴题．