题目内容
定义在R上的函数f(x)在区间(1,+∞)上是增函数,且函数F(x)=f(x+1)的图象关于y轴对称,则( )
| A、f(-1)>f(2) |
| B、f(0)>f(2) |
| C、f(-2)=f(2) |
| D、f(-4)=f(2) |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数奇偶性和单调性之间的关系,即可得到结论.
解答:
解:∵函数F(x)=f(x+1)的图象关于y轴对称,
∴f(-x+1)=f(x+1),
即f(x)关于x=1对称,
则f(-1)=f(3),f(0)=f(2),
∵函数f(x)在(1,+∞)上是增函数,
∴f(3)>f(2),
即f(-1)>f(2),
故选:A
∴f(-x+1)=f(x+1),
即f(x)关于x=1对称,
则f(-1)=f(3),f(0)=f(2),
∵函数f(x)在(1,+∞)上是增函数,
∴f(3)>f(2),
即f(-1)>f(2),
故选:A
点评:本题主要考查函数值的大小比较,根据函数奇偶性和单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
关于x的不等式(1+x)(2+x)>0的解集是( )
| A、{x|x<-1} |
| B、{x|x>-1或x<-2} |
| C、{x|x<1或x>2} |
| D、{x|-2<x<-1} |
已知数列{an}满足a1=1,an-an-1=3(n>1),则a10=( )
| A、27 | B、28 | C、29 | D、30 |
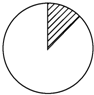 如图,有一圆盘,其中阴影部分的圆心角为45°,向圆盘内投镖,如果某人每次都投入圆盘内,那么他投中阴影部分的概率为
如图,有一圆盘,其中阴影部分的圆心角为45°,向圆盘内投镖,如果某人每次都投入圆盘内,那么他投中阴影部分的概率为 如图半圆O的直径为2,A点在直径的延长线上,且OA=2,B点为半圆周上的任意一点,以AB为边作一个等边△ABC,问B点在什么位置时,四边形OABC的面积最大?并求出此时的四边形面积.
如图半圆O的直径为2,A点在直径的延长线上,且OA=2,B点为半圆周上的任意一点,以AB为边作一个等边△ABC,问B点在什么位置时,四边形OABC的面积最大?并求出此时的四边形面积.