题目内容

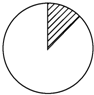如图，有一圆盘，其中阴影部分的圆心角为45°，向圆盘内投镖，如果某人每次都投入圆盘内，那么他投中阴影部分的概率为
 
．
考点：几何概型
专题：概率与统计
分析：由题意，所求属于几何概型；要计算投中阴影部分的概率，根据每次都投镖都能投入圆盘内，圆盘对应的圆心角的度数为360°，阴影部分的圆心角为45°，代入几何概型概率公式，即可得到答案．
解答： 解：圆盘对应的圆心角的度数为360°，
阴影部分的圆心角为45°
故投中阴影部分的概率P=
45
360
=
1
8
．
故答案为：
1
8
点评：本题考查了几何概型，找出所有基本事件对应的几何量是圆心角为360°的角度，满足条件的几何量是圆心角为45°的角度，是解答本题的关键，本题也可利用面积计算，即基本事件总数对应圆面积，满足条件的基本事件对应几何量为扇形面积．
练习册系列答案
相关题目
已知f（x）=
a
•
b
-1，其中向量
a
=（
3
sin2x，cosx），
b
=（1，2cosx）（x∈R）．
（1）求f（x）的单调递增区间；
（2）在△ABC中，角A、B、C的对边分别为a、b、c，f（A）=2，a=
3
，B=
π
4
，求边长b的值．
从某项综合能力测试中抽取100人的成绩（5分制），统计如表，则这100人成绩的方差为
 
．
成绩（分）543210 
人数5025101005 
已知数列{an}中，a1=2，a2=3，其前n项和Sn满足Sn+1+Sn-1=2Sn+1（n≥2，n∈N*．
（1）求数列{an}的通项公式；
（2）设bn=4n+（-1）n-1λ•2bn=4n+（-1）n-1λ•2 an（λ为非零整数，n∈N*），试确定λ的值，使得对任意n∈N*，都有bn+1＞bn成立．
半径为2，圆心角为
π
3
的扇形的面积为（　　）
A、
4π
3
B、π
C、
2π
3
D、
π
3
若关于x的不等式ax2+bx+2＞0的解集为(-
1
2
，
1
3
)，其中a，b为常数，则不等式2x2+bx+a＜0的解集是（　　）
A、（-3，2）
B、（-2，2）
C、（-2，3）
D、（-3，3）
定义在R上的函数f（x）在区间（1，+∞）上是增函数，且函数F（x）=f（x+1）的图象关于y轴对称，则（　　）
A、f（-1）＞f（2）
B、f（0）＞f（2）
C、f（-2）=f（2）
D、f（-4）=f（2）
下列结论正确的是（　　）
A、若ac≤bc，则a≤b
B、若a2≥b2，则a≥b
C、若a＜b，c＜0，则 a-c＞b-c
D、若
a
≥
b
，则a≥b
若函数f（x）=lnx，则f（
1
e
）的值是（　　）
A、eB、0C、-1D、1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网