题目内容
已知数列{an}满足a1=1，an-an-1=3（n＞1），则a10=（ ）
| A、27 | B、28 | C、29 | D、30 |
考点：等差数列的通项公式
专题：等差数列与等比数列
分析：易判数列{an}为首项为1公差为3的等差数列，由通项公式可得．
解答：
解：∵数列{an}满足a1=1，an-an-1=3（n＞1），
∴数列{an}为首项为1公差为3的等差数列，
∴a10=1+3（10-1）=28
故选：B
∴数列{an}为首项为1公差为3的等差数列，
∴a10=1+3（10-1）=28
故选：B
点评：本题考查等差数列的通项公式，涉及等差数列的判定，属基础题．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
定义在R上的函数f（x）在区间（1，+∞）上是增函数，且函数F（x）=f（x+1）的图象关于y轴对称，则（ ）
| A、f（-1）＞f（2） |
| B、f（0）＞f（2） |
| C、f（-2）=f（2） |
| D、f（-4）=f（2） |
当0＜x＜
时，函数f（x）=
的最小值为（ ）
| π |
| 2 |
| cos2x+cos2x+9sin2x |
| sin2x |
| A、2 | ||
B、2
| ||
| C、4 | ||
D、4
|
若函数f（x）=lnx，则f（
）的值是（ ）
| 1 |
| e |
| A、e | B、0 | C、-1 | D、1 |
函数f（x）=
，则f[f（
）]的值是（ ）
|
| 1 |
| 3 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
设z=1-i复数，则复数1+z2在复平面内所对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
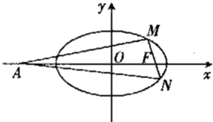如图所示，已知椭圆C：