题目内容
12.已知函数f(x)=$\left\{\begin{array}{l}{f(x-2),x>1}\\{{2}^{2{x}^{2}-1},x≤1}\end{array}\right.$,则f(3)=2;当x<0时,不等式f(x)<2的解集为(-1,0).分析 根据分段函数的表达式利用代入法即可求f(3),解不等式即可得到结论.
解答 解:由分段函数的表达式得f(3)=f(1)=22-1=2,
当x<0时,由f(x)<2得${2}^{2{x}^{2}-1}$<2,
即2x2-1<1,即2x2<2,x2<1,
得-1<x<1,此时-1<x<0,
即不等式的解集是(-1,0),
故答案为:2,(-1,0).
点评 本题主要考查分段函数的应用,利用代入法和直接法是解决本题的关键.比较基础.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
3.已知sinα+cosα=-$\sqrt{2}$,则tanα=( )
| A. | 1 | B. | -2+$\sqrt{3}$ | C. | -2-$\sqrt{3}$ | D. | 2±$\sqrt{3}$ |
20.已知集合P={x|1<x≤2},Q={x|x2-2x≥0},若U=R,则P∪∁UQ=( )
| A. | [0,2] | B. | (0,2] | C. | (1,2] | D. | [1,2] |
17.某工厂一年中各月份的收入、支出情况的统计如图所示,下列说法中错误的是( )
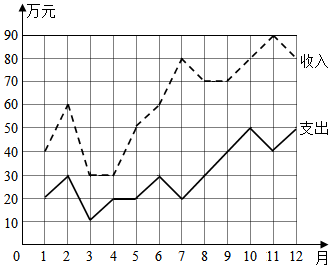
(注:结余=收入-支出)

(注:结余=收入-支出)
| A. | 收入最高值与收入最低值的比是3:1 | |
| B. | 结余最高的月份是7月 | |
| C. | 1至2月份的收入的变化率与4至5月份的收入的变化率相同 | |
| D. | 前6个月的平均收入为40万元 |
4.某班倡议假期每位学生至少阅读一本名著,为了解学生的阅读情况,对该班所有学生进行了调查.调查结果如表:
(Ⅰ)试根据上述数据,求这个班级女生阅读名著的平均本数;
(Ⅱ)若从阅读5本名著的学生中任选2人交流读书心得,求选到男生和女生各1人的概率;
(Ⅲ)试判断该班男生阅读名著本数的方差${s_1}^2$与女生阅读名著本数的方差${s_2}^2$的大小
(只需写出结论).(注:方差${s^2}=\frac{1}{n}[{({x_1}-\bar x)^2}+{({x_2}-\bar x)^2}+…+{({x_n}-\bar x)^2}]$,其中$\overline x$为x1x2,…xn的平均数)
| 阅读名著的本数 | 1 | 2 | 3 | 4 | 5 |
| 男生人数 | 3 | 1 | 2 | 1 | 3 |
| 女生人数 | 1 | 3 | 3 | 1 | 2 |
(Ⅱ)若从阅读5本名著的学生中任选2人交流读书心得,求选到男生和女生各1人的概率;
(Ⅲ)试判断该班男生阅读名著本数的方差${s_1}^2$与女生阅读名著本数的方差${s_2}^2$的大小
(只需写出结论).(注:方差${s^2}=\frac{1}{n}[{({x_1}-\bar x)^2}+{({x_2}-\bar x)^2}+…+{({x_n}-\bar x)^2}]$,其中$\overline x$为x1x2,…xn的平均数)
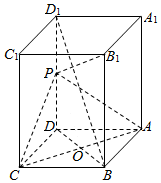 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,点P为DD1的中点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,点P为DD1的中点.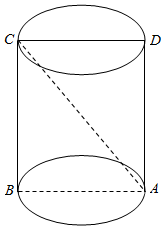 如图所示,已知圆柱的轴截面是一个正方形ABCD,圆柱的全面积为6πcm2,求
如图所示,已知圆柱的轴截面是一个正方形ABCD,圆柱的全面积为6πcm2,求