题目内容
2．
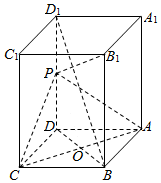如图，长方体ABCD-A1B1C1D1中，AB=AD=1，点P为DD1的中点．（1）求证：直线BD1∥平面PAC；
（2）求证：平面PAC⊥平面BDD1．
分析 （1）设AC和BD交于点O，连PO，则PO∥BD1，由此能证明直线BD1∥平面PAC．
（2）推导出AC⊥BD，DD1⊥AC，由此能证明平面PAC⊥平面BDD1．
解答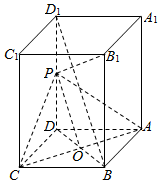 
证明：（1）设AC和BD交于点O，连PO，
由P，O分别是DD1，BD的中点，故PO∥BD1，
因为PO?平面PAC，BD1?平面PAC，
所以直线BD1∥平面PAC
（2）长方体ABCD-A1B1C1D1中，AB=AD=1，
底面ABCD是正方形，则AC⊥BD
又DD1⊥面ABCD，则DD1⊥AC，
所以AC⊥面BDD1，则平面PAC⊥平面BDD1．
点评 本题考查线面平行的证明，考查面面垂直的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
12．执行如图的程序框图（N∈N*），那么输出的p是（ ）
| A． | $A_{N+3}^{N+3}$ | B． | $A_{N+2}^{N+2}$ | C． | $A_{N+1}^{N+1}$ | D． | $A_N^N$ |
13．设复数z满足$\frac{1-z}{1+z}$=i，则z的虚部为（ ）
| A． | -2 | B． | 0 | C． | -1 | D． | 1 |