题目内容
2.设数列{an}的前n项和Sn=2an-a1,且a1,a2+1,a3成等差数列.(1)求数列{an}的通项公式;
(2)记数列$\{\frac{1}{a_n}\}$的前n项和Tn,求使得$|{T_n}-1|<\frac{1}{2016}$成立的n的最小值.
分析 (1)由已知Sn=2an-a1,有an=Sn-Sn-1=2an-2an-1(n>1),即an=2an-1(n>1).由a1,a2+1,a3成等差数列,即a1+a3=2(a2+1).解出即可得出.
(2)利用等比数列的前n项和公式及其不等式的性质即可得出.
解答 解:(1)∵Sn=2an-a1,∴an=Sn-Sn-1=2an-2an-1(n>1),
即an=2an-1(n>1).
从而a2=2a1,a3=4a1,
又∵a1,a2+1,a3成等差数列,即a1+a3=2(a2+1).
∴a1+4a1=2(2a1+1),解得a1=2.
∴数列{an}是首项为2,公比为2的等比数列.
故${a_n}={2^n}$.
(2)由(1)得$\frac{1}{a_n}=\frac{1}{2^n}$.
∴${T_n}=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{2^n}=\frac{{\frac{1}{2}[1-{{(\frac{1}{2})}^n}]}}{{1-\frac{1}{2}}}=1-\frac{1}{2^n}$.
由$|{T_n}-1|<\frac{1}{2016}$,得$|1-\frac{1}{2^n}-1|<\frac{1}{2016}$,即2n>2016.
∵210=1024<2016<2048=211,
∴n≥11.
于是,使$|{T_n}-1|<\frac{1}{2016}$成立的n的最小值为11.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.已知复数z1、z2在复平面内对应的点分别为A(1,-1)、B(3,1),则$\frac{z_2}{z_1}$=( )
| A. | 1+2i | B. | 2+i | C. | 1+3i | D. | 3+i |
12.一个三层书架,分别放置语文书12本,数学书14本,英语书11本,从中取出语文、数学、英语各一本,则不同的取法共有( )
| A. | 37种 | B. | 1848种 | C. | 3种 | D. | 6种 |





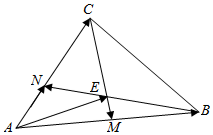 如图所示,在△ABC中,点M为AB的中点,且AN=$\frac{1}{2}$NC,BN与CM相交于点E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试以$\overrightarrow{a}$,$\overrightarrow{b}$为基底表示$\overrightarrow{AE}$.
如图所示,在△ABC中,点M为AB的中点,且AN=$\frac{1}{2}$NC,BN与CM相交于点E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试以$\overrightarrow{a}$,$\overrightarrow{b}$为基底表示$\overrightarrow{AE}$.