题目内容
在△ABC中,内角A、B、C所对的边分别为a、b、c,且A、B、C成等差数列.
(1)若b=
,求a+c的取值范围;
(2)若
,
,
也成等差数列,求A、C的大小.
(1)若b=
| ||
| 2 |
(2)若
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
考点:余弦定理,等差数列的性质
专题:三角函数的求值
分析:(1)由A、B、C成等差数列,利用等差数列的性质求出B的度数,得到sinB的值,再由b的值,利用正弦定理表示出a与c,代入a+c中,用A表示出B,利用两角和与差的正弦函数公式化为一个角的正弦函数,利用正弦函数的值域即可确定出a+c的范围;
(2)由
,
,
成等差数列,利用等差数列的性质列出关系式,再利用正弦定理化简,将sinB的值代入,利用和差化积公式变形,设cos
=t,得到关于t的方程,求出方程的解得到t的值,即为cos
的值,即可确定出A与C的度数.
(2)由
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| A-C |
| 2 |
| A-C |
| 2 |
解答:
解:(1)∵A、B、C成等差数列,
∴2B=A+C,
∵A+B+C=π,
∴B=
,A+C=
,
∵b=
,
∴由正弦定理
=
=
=
=1,即a=sinA,c=sinC,
∴a+c=sinA+sinC=sinA+sin(
-A)=sinA+
cosA+
sinA=
sinA+
cosA=
(
sinA+
cosA)=
sin(A+
),
∵0<A<
,∴
<A+
<
,
∴
<sin(A+
)≤1,即
<
sin(A+
)≤
,
则a+c的范围为(
,
];
(2)∵
,
,
成等差数列,
∴
=
+
,
∴由正弦定理化简得:
+
=
=
,
整理得:sinA+sinC
sinAsinC,
∴2sin
cos
=-
×
[cos(A+C)-cos(A-C)],
即
cos
+
[-
-cos(A-C)]=0,
设cos
=t,则有3t-1-2(2t2-1)=0,
整理得:(4t+1)(t-1)=0,
解得:t=-
(舍去)或t=1,
∴cos
=1,即A-C=0,
∴A=C=B=60°.
∴2B=A+C,
∵A+B+C=π,
∴B=
| π |
| 3 |
| 2π |
| 3 |
∵b=
| ||
| 2 |
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| ||||
|
∴a+c=sinA+sinC=sinA+sin(
| 2π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| π |
| 6 |
∵0<A<
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
| 3 |
| π |
| 6 |
| 3 |
则a+c的范围为(
| ||
| 2 |
| 3 |
(2)∵
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
∴
| 2 |
| b |
| 1 |
| a |
| 1 |
| c |
∴由正弦定理化简得:
| 1 |
| sinA |
| 1 |
| sinC |
| 2 | ||
sin
|
| 4 | ||
|
整理得:sinA+sinC
| 4 | ||
|
∴2sin
| A+C |
| 2 |
| A-C |
| 2 |
| 4 | ||
|
| 1 |
| 2 |
即
| 3 |
| A-C |
| 2 |
| 2 | ||
|
| 1 |
| 2 |
设cos
| A-C |
| 2 |
整理得:(4t+1)(t-1)=0,
解得:t=-
| 1 |
| 4 |
∴cos
| A-C |
| 2 |
∴A=C=B=60°.
点评:此题考查了正弦、余弦定理,等差数列的性质,以及同角三角函数间的基本关系,熟练掌握定理是解本题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
给出下列四个命题,其中假命题是( )
| A、从匀速传递的新产品生产流水线上,质检员每10分钟从中抽取一件新产品进行某项指标检测,这样的抽样是分层抽样 | ||
| B、样本方差反映了样本数据与样本平均值的偏离程度 | ||
| C、在回归分析模型中,残差平方和越小,说明模型的拟合效果越好 | ||
D、设随机变量X服从正态分布N(0,1),若P(x>1)=p,则P(-1<x<0)=
|
 如图,三行三列的方阵中有9个数aij(i=1,2,3;j=1,2,3),从中任取三个数,则这三个数位于不同行不同列的概率是
如图,三行三列的方阵中有9个数aij(i=1,2,3;j=1,2,3),从中任取三个数,则这三个数位于不同行不同列的概率是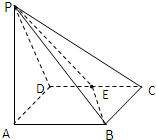 如图,四棱锥P-ABCD中,ABCD为菱形,PA⊥平面ABCD,∠BCD=60°,BC=1,E为CD的中点,PC与平面ABCD成角60°
如图,四棱锥P-ABCD中,ABCD为菱形,PA⊥平面ABCD,∠BCD=60°,BC=1,E为CD的中点,PC与平面ABCD成角60°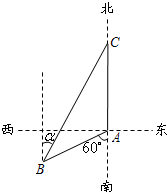 如图所示,海监船位于岛屿A的南偏西60°方向且与岛屿A相距12海里的B处,一艘不明身份的渔船从岛屿A出发沿正北方向以10海里/小时的速度航行.若海监船同时从B处出发,沿北偏东的方向以20海里/小时的速度尽快追赶渔船予以查处.则海监船最少约用多长时间能追上渔船?
如图所示,海监船位于岛屿A的南偏西60°方向且与岛屿A相距12海里的B处,一艘不明身份的渔船从岛屿A出发沿正北方向以10海里/小时的速度航行.若海监船同时从B处出发,沿北偏东的方向以20海里/小时的速度尽快追赶渔船予以查处.则海监船最少约用多长时间能追上渔船?