题目内容
求函数y=tan2x+tanx-1(|x|≤
)的值域.
| π |
| 4 |
考点:三角函数的最值
专题:三角函数的图像与性质
分析:对所求函数配方可得y=(tanx+
)2-
,结合二次函数在该区间上的单调性判值域.
| 1 |
| 2 |
| 5 |
| 4 |
解答:
解:由|x|≤
,∴tanx∈[-1,1]
y=tan2x+tanx-1=(tanx+
)2-
在[-
,1]单调递增,在[-1,-
]上单调减,
∴-
≤y≤1,
函数y=tan2x+tanx-1(|x|≤
)的值域为[-
,1].
| π |
| 4 |
y=tan2x+tanx-1=(tanx+
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
∴-
| 5 |
| 4 |
函数y=tan2x+tanx-1(|x|≤
| π |
| 4 |
| 5 |
| 4 |
点评:本题综合考查三角不等式的解法及二次函数的值域的求解,关键是要注意二次函数在所给区间上的单调性,准确判断取得最值的位置.

练习册系列答案
相关题目
已知集合A={x∈R||x|≤2},B={x|
≥1},则A∩B=( )
| 1 |
| x-1 |
| A、[1,2] |
| B、[-2,1) |
| C、(1,2] |
| D、[-2,1]∪{2} |
 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥面ABCD,PA=PB=2.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥面ABCD,PA=PB=2.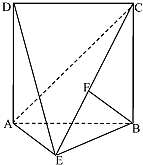 如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,动点F在校CE上,无论点F运动到何处时,总有BF⊥AE.
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,动点F在校CE上,无论点F运动到何处时,总有BF⊥AE.