题目内容
 已知一正整数的数阵如图所示(从上至下第1行是1,第二行是3,、2,…),则自上而下,第100行第2个数是
已知一正整数的数阵如图所示(从上至下第1行是1,第二行是3,、2,…),则自上而下,第100行第2个数是考点:归纳推理
专题:计算题,推理和证明
分析:根据奇数行,依次增加1,偶数行,依次减少1,每行正整数的个数与行数相同,即可得到结论.
解答:
解:由于每行正整数的个数与行数相同,
且最大数为:1+2+3+••+n=
,
又奇数行,依次增加1,偶数行,依次减少1,
则第100行第2个数为:
-1=5049.
故答案为:5049.
且最大数为:1+2+3+••+n=
| n(n+1) |
| 2 |
又奇数行,依次增加1,偶数行,依次减少1,
则第100行第2个数为:
| 100×101 |
| 2 |
故答案为:5049.
点评:本题考查数列的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
等比数列{an}的首项a1=-1,前n项和为Sn若
=
,则公比q等于( )
| S 10 |
| S 5 |
| 31 |
| 32 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
函数y=
是( )
| |x| | ||
|
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数,又是偶函数 |
| D、既不是奇函数,也不是偶函数 |
下列函数中,在R上是增函数的是( )
| A、y=-x+1 | ||
| B、y=-x2 | ||
C、y=
| ||
| D、y=x3 |
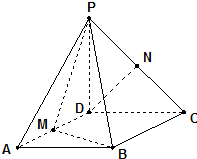 已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形且PD=AD=2,又PD⊥底面ABCD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形且PD=AD=2,又PD⊥底面ABCD,点M、N分别是棱AD、PC的中点.