题目内容
函数y=
是（ ）
| |x| | ||
|
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数，又是偶函数 |
| D、既不是奇函数，也不是偶函数 |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：求出原函数的定义域，然后利用f（-x）=f（x）得答案．
解答：
解：由1-x2＞0，得-1＜x＜1．
∴函数y=
的定义域为（-1，1）．
又f（-x）=
=
=f(x)．
∴函数y=
是偶函数．
故选：B．
∴函数y=
| |x| | ||
|
又f（-x）=
| |-x| | ||
|
| |x| | ||
|
∴函数y=
| |x| | ||
|
故选：B．
点评：本题考查了函数奇偶性的判断，关键是注意函数的定义域，是基础题．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
已知一正整数的数阵如图所示（从上至下第1行是1，第二行是3，、2，…），则自上而下，第100行第2个数是执行如图的程序框图，若输入的P是10，则输出的结果S的值为（ ）
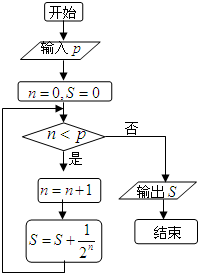
A、1-
| ||
B、1-
| ||
C、1-
| ||
D、10-
|
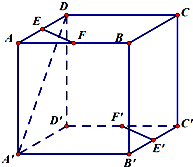如图，在正方体AC′中，E，F，E′，F′分别是AD，AB，B′C′，D′C′的中点．