题目内容
若数列{an}前n项和可表示为Sn=2n+a,则{an}是否可能成为等比数列?若可能,求出a值;若不可能,说明理由.
考点:数列的求和
专题:等差数列与等比数列
分析:首先利用前n项和Sn=2n+a整理出an=2n+a-2n-1-a=2n-1,进一步利用特殊项求出a的值,最后利用分类讨论说明结论:当a=-1时,数列{an}成等比数列,首项为1,公比为2,当a≠-1时,{an}不是等比数列.
解答:
解:因{an}的前n项和Sn=2n+a,故a1=S1=2+a,an=Sn-Sn-1(n≥2),
an=2n+a-2n-1-a=2n-1(n≥2),
要使a1适合n≥2时的通项公式,则必有:2+a=2°则:a=-1,
此时an=2n-1(n∈N+),
q=
=
=2,
故当a=-1时,数列{an}成等比数列,首项为1,公比为2,当a≠-1时,{an}不是等比数列;
故答案为:当a=-1时,数列{an}成等比数列,首项为1,公比为2,
当a≠-1时,{an}不是等比数列.
an=2n+a-2n-1-a=2n-1(n≥2),
要使a1适合n≥2时的通项公式,则必有:2+a=2°则:a=-1,
此时an=2n-1(n∈N+),
q=
| an+1 |
| an |
| 2n |
| 2n-1 |
故当a=-1时,数列{an}成等比数列,首项为1,公比为2,当a≠-1时,{an}不是等比数列;
故答案为:当a=-1时,数列{an}成等比数列,首项为1,公比为2,
当a≠-1时,{an}不是等比数列.
点评:本题考查的知识点:求数列的方法:前n项和法,及相关的分类讨论问题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
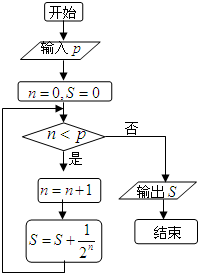
执行如图的程序框图,若输入的P是10,则输出的结果S的值为( )

A、1-
| ||
B、1-
| ||
C、1-
| ||
D、10-
|
过点(-l,3)且与直线x-2y+3=0垂直的直线方程是( )
| A、x-2y+7=0 |
| B、2x-y+5=0 |
| C、2x+y-5=0 |
| D、2x+y-1=0 |

 已知一正整数的数阵如图所示(从上至下第1行是1,第二行是3,、2,…),则自上而下,第100行第2个数是
已知一正整数的数阵如图所示(从上至下第1行是1,第二行是3,、2,…),则自上而下,第100行第2个数是