题目内容
动点P到点F(1,0)和直线x=-1的距离相等,直线l:kx-y-1=0与点P的轨迹C交于A,B两点
(1)求 P点的轨迹C的方程;
(2)当k变化时,求
•
最小值.
(1)求 P点的轨迹C的方程;
(2)当k变化时,求
| OA |
| OB |
考点:轨迹方程,平面向量数量积的运算
专题:向量与圆锥曲线
分析:(1)设出P点坐标,由题意列等式,化简后得答案;
(2)联立直线方程和抛物线方程,化为关于x的一元二次方程,利用根与系数关系得到A,B两点的横纵坐标的积,由判别式大于0求得k的范围,然后利用配方法求得
•
的范围.
(2)联立直线方程和抛物线方程,化为关于x的一元二次方程,利用根与系数关系得到A,B两点的横纵坐标的积,由判别式大于0求得k的范围,然后利用配方法求得
| OA |
| OB |
解答:
解:(1)设动点P的坐标为(x,y),依题意,得|PF|=|x+1|,
即
=|x+1|,
化简得:y2=4x,
∴曲线C1的方程为y2=4x;
(2)联立
,得k2x2-(2k+4)x+1=0.
由△=(2k+4)2-4k2=16k+16>0,得k>-1.
设A(x1,y1),B(x2,y2),
则x1+x2=
,x1x2=
,
y1y2=(kx1-1)(kx2-1)=k2x1x2-k(x1+x2)+1
=k2•
-k•
+1=1-
+1=-
.
∴
•
=x1x2+y1y2=
-
=(
-2)2-4.
∵k>-1,∴
<-1,
∴
•
=(
-2)2-4>5.
即
•
的范围是(5,+∞).
即
| (x-1)2+y2 |
化简得:y2=4x,
∴曲线C1的方程为y2=4x;
(2)联立
|
由△=(2k+4)2-4k2=16k+16>0,得k>-1.
设A(x1,y1),B(x2,y2),
则x1+x2=
| 2k+4 |
| k2 |
| 1 |
| k2 |
y1y2=(kx1-1)(kx2-1)=k2x1x2-k(x1+x2)+1
=k2•
| 1 |
| k2 |
| 2k+4 |
| k2 |
| 2k+4 |
| k |
| 4 |
| k |
∴
| OA |
| OB |
| 1 |
| k2 |
| 4 |
| k |
| 1 |
| k |
∵k>-1,∴
| 1 |
| k |
∴
| OA |
| OB |
| 1 |
| k |
即
| OA |
| OB |
点评:本题考查了轨迹方程的求法,考查了直线和抛物线的关系,训练了平面向量数量积的应用,考查了利用配方法求函数的最值,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设集合A={x|x2-x=0},B={x|x2+x=0},则集合A∪B=( )
| A、0 | B、{0} |
| C、∅ | D、{-1,0,1} |
设动点A、B均在双曲线C:
-
=1(a>0,b>0)的右支上,点O为坐标原点,双曲线C的离心率为e,则( )
| x2 |
| a2 |
| y2 |
| b2 |
A、若e>
| ||||||
B、若1≤e≤
| ||||||
C、若e>
| ||||||
D、若1<e≤
|
已知函数f(x)=
则方程f(x)=1解的个数为( )
|
| A、1 | B、2 | C、3 | D、4 |
已知|F1F2|=m,点P到两点F1、F2距离之差的绝对值为n(n<m).设点P的轨迹为C,过F1作AB⊥F1F2且交曲线C于点A、B,若△ABF2是直角三角形,则
的值为( )
| m |
| n |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
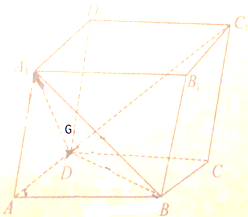 如图,在平行六面体ABCD-A1B1C1D1中,G为△A1BD的重心,设
如图,在平行六面体ABCD-A1B1C1D1中,G为△A1BD的重心,设 如图,正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是线段AD1和B1C上的动点,且满足AP=B1Q,则下列命题正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是线段AD1和B1C上的动点,且满足AP=B1Q,则下列命题正确的是