题目内容
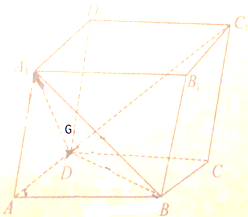如图，在平行六面体ABCD-A1B1C1D1中，G为△A1BD的重心，设| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| a |
| b |
| c |
| AC1 |
| AG |
考点：平面向量的基本定理及其意义
专题：空间向量及应用
分析：将体对角线
用基底表示，然后利用向量加法的三角形法则及重心的性质，将
用基底表示．
| AC1 |
| AG |
解答：
解：在平行六面体ABCD-A1B1C1D1中，
=
+
=
+
+
=
+
+
，
∵G为△A1BD的重心，
∴
=
×
（
+
）=
（
-
+
-
）=
（
+
-2
）=
+
-
．
| AC1 |
| AC |
| CC1 |
| AB |
| AD |
| AA1 |
| a |
| b |
| c |
∵G为△A1BD的重心，
∴
| A1G |
| 2 |
| 3 |
| 1 |
| 2 |
| A1B |
| A1D |
| 1 |
| 3 |
| AB |
| AA1 |
| AD |
| AA1 |
| 1 |
| 3 |
| a |
| b |
| c |
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| 2 |
| 3 |
| c |
点评：本题考查了空间向量的基本定理及其应用，向量加法的三角形法则，重心的性质．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
在集合{a，b，c，d}上定义两种运算⊕和?如下：
那么d?（a⊕c）=（ ）
那么d?（a⊕c）=（ ）
| A、a | B、b | C、c | D、d |
已知f（x）为R上的偶函数，且f（1）=0，当x1，x2∈[0，+∞）且x1＜x2时，有f（x1）＜f（x2），则不等式
＜0的解为（ ）
| f(x)+2•f(-x) |
| x |
| A、（-1，1） |
| B、（-∞，-1）∪（1，+∞） |
| C、（-∞，-1）∪（0，1） |
| D、（-1，0）∪（1，+∞） |