题目内容
不等式ax2-x-c>0的解集为{x|-2<x<1},则函数y=ax2+x-c的零点为( )
| A、(-1,0)和(2,0) |
| B、(-1,0) |
| C、(2,0) |
| D、-1和2 |
考点:一元二次不等式的解法,函数零点的判定定理
专题:不等式的解法及应用
分析:根据不等式ax2-x-c>0的解集,求出a、c的值,再求函数y=ax2+x-c的零点.
解答:
解:∵不等式ax2-x-c>0的解集为{x|-2<x<1},
∴a<0,且方程ax2-x-c=0的两个实数根是-2和1,
由根与系数的关系,得
;
解得a=-1、c=2,
∴函数y=ax2+x-c为y=-x2+x-2,
它的零点为2、-1.
故选:D.
∴a<0,且方程ax2-x-c=0的两个实数根是-2和1,
由根与系数的关系,得
|
解得a=-1、c=2,
∴函数y=ax2+x-c为y=-x2+x-2,
它的零点为2、-1.
故选:D.
点评:本题考查了一元二次不等式的解集以及二次函数与对应的方程之间的关系,解题时应根据根与系数的关系进行解答,是基础题.

练习册系列答案
相关题目
已知点P的极坐标是(2,π),则过点P且垂直极轴的直线方程是( )
| A、p=2 | ||
| B、p=2cosθ | ||
C、p=-
| ||
D、p=
|
某地铁的到站时间间隔是5分钟.某人进站到达列车门口等车时间超过2分钟的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
两位老师和两位同学站成一排合影,则两位老师至少有一人站在两端的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
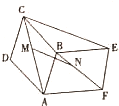 如图所示,ABCD-ABEF都是平行四边形,且不共面,M、N分别是AC、BF的中点,判断
如图所示,ABCD-ABEF都是平行四边形,且不共面,M、N分别是AC、BF的中点,判断