题目内容
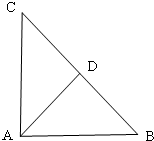
如图，在△ABC中，AD是高线，CE是中线，|DC|=|BE|，DG⊥CE于G，且|EC|=8，则|EG|= ．
考点：相似三角形的性质
专题：选作题,立体几何
分析：根据直角三角形的性质可得：|ED|=|BE|，即可得到|ED|=|DC|，结合DG⊥CE于G，可得线段CG垂直并且平分线段CE，进而求出答案．
解答：
解：因为AD是高线，CE是中线，
所以|ED|=|BE|，
因为|DC|=|BE|，
所以|ED|=|DC|．
又因为DG⊥CE于G，
所以线段CG垂直并且平分线段CE．
因为|EC|=8，
所以|EG|=4．
故答案为：4．
所以|ED|=|BE|，
因为|DC|=|BE|，
所以|ED|=|DC|．
又因为DG⊥CE于G，
所以线段CG垂直并且平分线段CE．
因为|EC|=8，
所以|EG|=4．
故答案为：4．
点评：本题考查直角三角形斜边上中线性质，等腰三角形性质等知识点，属于基础题．
练习册系列答案
相关题目
如图△ABC是直角边等于4的等腰直角三角形，D是斜边BC的中点，下列选项正确的是（ ）
| A、映射一定是函数 |
| B、一一映射一定是函数 |
| C、函数一定是一一映射 |
| D、函数一定是映射 |