题目内容
 已知如图所示是函数y=Asin(ωx+φ)的部分图象.
已知如图所示是函数y=Asin(ωx+φ)的部分图象.(1)求函数的解析式;
(2)求函数的单调区间;
(3)求不等式y≥2的解集.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)由函数的顶点坐标可得A=2,再根据周期求得ω=2,再由五点法作图求得φ=
,从而求得函数的解析式.
(2)令2kπ-
≤2x+
≤2kπ+
,求得x的范围,可得函数的增区间.令2kπ+
≤2x+
≤2kπ+
,求得≤x的范围,可得函数的减区间.
(3)由y≥2,可得sin(2x+
)=1,2x+
=2kπ+
,k∈z.求得x的值,可得不等式的解集.
| π |
| 6 |
(2)令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
(3)由y≥2,可得sin(2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
解答:
解:(1)由函数的顶点坐标可得A=2,又
•T=
•
=
-
,解得ω=2;
再由五点法作图可得 2×
+φ=
,φ=
,
故函数的解析式为y=2sin(2x+
).
(2)令2kπ-
≤2x+
≤2kπ+
,求得 kπ-
≤x≤kπ+
,k∈z,故函数的增区间为[kπ-
,kπ+
],k∈z.
令2kπ+
≤2x+
≤2kπ+
,求得 kπ+
≤x≤kπ+
,k∈z,故函数的减区间为[kπ+
,kπ+
],k∈z.
(3)由y≥2,可得2sin(2x+
)≥2,
∴sin(2x+
)≥1,又sin(2x+
)≤1,
∴sin(2x+
)=1,∴2x+
=2kπ+
,k∈z.
解得:x=kπ+
,k∈z,故不等式的解集为{x|x=kπ+
,k∈z }.
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| ω |
| 2π |
| 3 |
| π |
| 6 |
再由五点法作图可得 2×
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
故函数的解析式为y=2sin(2x+
| π |
| 6 |
(2)令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
令2kπ+
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
(3)由y≥2,可得2sin(2x+
| π |
| 6 |
∴sin(2x+
| π |
| 6 |
| π |
| 6 |
∴sin(2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
解得:x=kπ+
| π |
| 6 |
| π |
| 6 |
点评:本题主要考查y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
已知复数z满足z(1-i)=2i,其中i为虚数单位,则|z|=( )
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
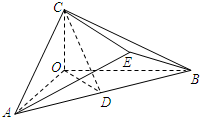 如图,在三棱锥C-OAB中,CO⊥平面AOB,OA=OB=2OC=2,AB=2
如图,在三棱锥C-OAB中,CO⊥平面AOB,OA=OB=2OC=2,AB=2