题目内容
已知盒中有10个灯泡,其中8个正品,2个次品.需要从中取出2个正品,每次取出1个,取出后不放回,直到取出2个正品为止.设ξ为取出的次数,求P(ξ=4)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:由题意知每次取1件产品,至少需2次,即ξ最小为2,有2件次品,当前2次取得的都是次品时ξ=4,得到变量的取值,当变量是2时,表示第一次取出正品,第二次取出也是正品,根据相互独立事件同时发生的概率公式可求得.
解答:
解:由题意知每次取1件产品,
∴至少需2次,即ξ最小为2,有2件次品,
当前2次取得的都是次品时,ξ=4,
∴ξ可以取2,3,4
当变量是2时,表示第一次取出正品,第二次取出也是正品,
根据相互独立事件同时发生的概率公式得到:
p(ξ=2)=
×
=
,
p(ξ=3)=
×
×
+
×
×
=
,
p(ξ=4)=1-
-
=
.
故选B.
∴至少需2次,即ξ最小为2,有2件次品,
当前2次取得的都是次品时,ξ=4,
∴ξ可以取2,3,4
当变量是2时,表示第一次取出正品,第二次取出也是正品,
根据相互独立事件同时发生的概率公式得到:
p(ξ=2)=
| 8 |
| 10 |
| 7 |
| 9 |
| 28 |
| 45 |
p(ξ=3)=
| 8 |
| 10 |
| 2 |
| 9 |
| 7 |
| 8 |
| 2 |
| 10 |
| 8 |
| 9 |
| 7 |
| 8 |
| 14 |
| 45 |
p(ξ=4)=1-
| 28 |
| 45 |
| 14 |
| 45 |
| 1 |
| 15 |
故选B.
点评:本题考查离散型随机变量的分布列和数学期望的概念,考查运用概率知识解决实际问题的能力.遇到求用至少来表述的事件的概率时,往往先求它的对立事件的概率.

练习册系列答案
相关题目
下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A、y=ln|x| |
| B、y=-x2 |
| C、y=ex |
| D、y=cosx |
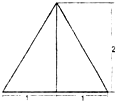 一个三棱锥的侧棱长都相等,底面是正三角形,其正(主)视图如右图所示.该三棱锥侧面积和体积分别是( )
一个三棱锥的侧棱长都相等,底面是正三角形,其正(主)视图如右图所示.该三棱锥侧面积和体积分别是( )A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、8,
|
tanθ和tan(
-θ)是方程x2+px+q=0的两根,则p与q的关系是( )
| π |
| 4 |
| A、p+q+1=0 |
| B、p+q-1=0 |
| C、p-q+1=0 |
| D、p-q-1=0 |
在△ABC中,根据下列条件解三角形,其中有两个解的是( )
| A、b=10,A=45°,C=60° |
| B、a=6,c=5,B=60° |
| C、a=7,b=5,A=60° |
| D、a=14,b=16,A=45° |
某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )


A、f(x)=
| ||||
B、f(x)=ln(
| ||||
C、f(x)=
| ||||
D、f(x)=
|
函数y=f(x)为偶函数,且[0,+∞)上单调递减,则y=f(2-x2)的一个单调递增区间为( )
| A、(-∞,0] | ||
| B、[0,+∞) | ||
C、[0,
| ||
D、[
|
已知数列{an}满足 a1=1,an=1+
,则 a5=( )
| 1 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
| D、2 |