题目内容
通过随机询问110名性别不同的大学生是否爱好某项运动,其中60名男大学生中有40人爱好此项运动,女大学生中有20人爱好此项运动,其中K2=
,附表:
能不能有99%以上的把握认为“爱好该项运动与性别有关”
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
考点:独立性检验
专题:计算题,概率与统计
分析:由K2=
公式代入数据从而查表得出概率.
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
解答:
解:假设:爱好该项运动与性别无关,
∵K2=
=
≈0.524<6.635.
故没有99%以上的把握认为“爱好该项运动与性别有关”.
∵K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
=
| 110×(20×30-40×20)2 |
| 60×50×40×70 |
故没有99%以上的把握认为“爱好该项运动与性别有关”.
点评:本题考查了学生对独立性检验的掌握,属于基础题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
设tanα=3,则
=( )
| sin(α-π)+cos(π-α) | ||||
sin(
|
| A、3 | B、2 | C、1 | D、-1 |
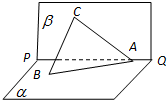 已知直二面角α-PQ-β,A∈PQ,B∈α,C∈β,CA=CB,∠BAP=45°,直线CA和平面α所成的角为30°.
已知直二面角α-PQ-β,A∈PQ,B∈α,C∈β,CA=CB,∠BAP=45°,直线CA和平面α所成的角为30°.