题目内容
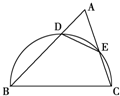如图，锐角三角形ABC中，以BC为直径的半圆分别交AB、AC于点D、E，则△ADE与△ABC的面积之比为（ ）| A、cosA |
| B、sinA |
| C、sin2A |
| D、cos2A |
考点：圆內接多边形的性质与判定
专题：选作题,立体几何
分析：连接BE．构建直角△ABE，通过解该直角三角形求得cosA=
；然后通过相似三角形△AED∽△ABC的对应边的比成比例知
=
；最后结合三角形的面积公式分别求得△ADE、△ABC的面积．
| AE |
| AB |
| AE |
| AB |
| AD |
| AC |
解答：
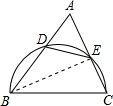解：如图，连接BE．
∵BC为半圆的直径，
∴∠BEC=∠AEB=90°．
∴在直角△ABE中，cosA=
，
∵点D、B、C、E四点共圆，
∴∠ABC+∠DEC=180°．
∵∠DEC+∠AED=180°，
∴∠ABC=∠AED．
又∵∠A=∠A，
∴△AED∽△ABC，
∴
=
．
∵S△ADE=
AE•AD•sinA，S△ABC=
AB•AC•sinA，
∴S△ADE：S△ABC=
=
=cos2A．
故选：D．
解：如图，连接BE．∵BC为半圆的直径，
∴∠BEC=∠AEB=90°．
∴在直角△ABE中，cosA=
| AE |
| AB |
∵点D、B、C、E四点共圆，
∴∠ABC+∠DEC=180°．
∵∠DEC+∠AED=180°，
∴∠ABC=∠AED．
又∵∠A=∠A，
∴△AED∽△ABC，
∴
| AE |
| AB |
| AD |
| AC |
∵S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ADE：S△ABC=
| AE•AD |
| AB•AC |
| AE2 |
| AB2 |
故选：D．
点评：本题考查了相似三角形的判定与性质、圆周角定理以及解直角三角形等知识点．解答该题时，借用了圆内接四边形的内对角互补的性质．
练习册系列答案
名校课堂系列答案
相关题目
要得到函数y=
cosx的图象，只要将函数y=
sin（x+
）的图象（ ）
| 2 |
| 2 |
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
不等式
≤0的实数解为（ ）
| x-20 |
| x+16 |
| A、-20≤x≤16 |
| B、-16≤x≤20 |
| C、-16＜x≤20 |
| D、x＜-16或x≥20 |
命题“若a＞b，则2a＞2b-1”的否命题为（ ）
| A、若a＞b，则有2a≤2b-1 |
| B、若a≤b，则有2a≤2b-1 |
| C、若a≤b，则有2a＞2b-1 |
| D、若2a≤2b-1，则有a≤b |
2014年某通讯公司推出一组手机卡号码，卡号的前七位数字固定，后四位数从“0000”到“9999”共10000个号码．公司规定：凡卡号的后四位带数字“5”或“8”的一律作为“金马卡”，享受一定优惠政策，则这组号码中“金马卡”的个数为（ ）
| A、2000 | B、4096 |
| C、5904 | D、8320 |
三个数a=20.5，b=（
）2，c=log2
的大小关系是（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、a＜b＜c |
| B、b＜a＜c |
| C、c＜b＜a |
| D、a＜c＜b |
数列{an}的通项公式为an=n2+1，则a5的值为（ ）
| A、5 | B、10 | C、17 | D、26 |