题目内容
三个数a=20.5,b=(
)2,c=log2
的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<b<c |
| B、b<a<c |
| C、c<b<a |
| D、a<c<b |
考点:不等式比较大小,对数值大小的比较
专题:函数的性质及应用
分析:利用指数函数、对数函数的单调性即可得出.
解答:
解:∵a=20.5>20=1,0<b=(
)2<(
)0=1,c=log2
<0.
∴a>b>c.
故选:C.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴a>b>c.
故选:C.
点评:本题考查了指数函数、对数函数的单调性,属于基础题.

练习册系列答案
相关题目
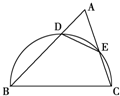 如图,锐角三角形ABC中,以BC为直径的半圆分别交AB、AC于点D、E,则△ADE与△ABC的面积之比为( )
如图,锐角三角形ABC中,以BC为直径的半圆分别交AB、AC于点D、E,则△ADE与△ABC的面积之比为( )| A、cosA |
| B、sinA |
| C、sin2A |
| D、cos2A |
函数f(x)=
,满足f(x)>1的x的取值范围是( )
|
| A、(-1,10) |
| B、(-1,+∞) |
| C、{x|x>10或x<-2} |
| D、{x|x>10或x<-1} |
下列说法正确的是( )
| A、相关指数R2越大的模型,拟合效果越好 |
| B、回归直线的斜率都大于零 |
| C、相关系数r越大,线性相关性越强 |
| D、相关系数r∈(-1,1) |
函数f(x)=log3x在(3,1)处的导数为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
甲、乙、丙等五人站成一排,要求甲、乙均不与丙相邻,则不同的排法为( )
| A、72 | B、36 | C、52 | D、24 |
将5名大学毕业生全部分配给3所不同的学校,不同的分配方式的种数有( )
| A、8 | B、15 | C、125 | D、243 |
若等差数列{an}满足:
<-1,且其前n项和Sn有最大值.则当数列Sn>0时,n的值为( )
| a11 |
| a12 |
| A、20 | B、21 | C、23 | D、22 |