题目内容
不等式
≤0的实数解为（ ）
| x-20 |
| x+16 |
| A、-20≤x≤16 |
| B、-16≤x≤20 |
| C、-16＜x≤20 |
| D、x＜-16或x≥20 |
考点：其他不等式的解法
专题：不等式的解法及应用
分析：将分式不等式进行转化即可得到结论．
解答：
解：不等式等价为
，
即
，
即-16＜x≤20，
故选：C
|
即
|
即-16＜x≤20，
故选：C
点评：本题主要考查不等式的解法，将分式不等式转化为整式不等式是解决本题的基本方法．
练习册系列答案
全能测控期末小状元系列答案
相关题目
复数（i+1）i的共轭复数是（ ）
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
下列向量中不是单位向量的是（ ）
| A、（-1，0） | ||||||||
| B、（1，1） | ||||||||
| C、（cosa，sina） | ||||||||
D、
|
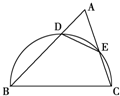如图，锐角三角形ABC中，以BC为直径的半圆分别交AB、AC于点D、E，则△ADE与△ABC的面积之比为（ ）| A、cosA |
| B、sinA |
| C、sin2A |
| D、cos2A |
有一段演绎推理是这样的“任何实数的平方都大于0，因为a∈R，所以a2＞0”结论显然是错误的，是因为（ ）
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、非以上错误 |
下列说法正确的是（ ）
| A、相关指数R2越大的模型，拟合效果越好 |
| B、回归直线的斜率都大于零 |
| C、相关系数r越大，线性相关性越强 |
| D、相关系数r∈（-1，1） |
已知正四面体A-BCD棱长都为
，M为AC中点，N为CD中点，求异面直线BM与AN所成角的余弦值（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|