题目内容

要得到函数y=
2
cosx的图象，只要将函数y=
2
sin（x+
π
4
）的图象（　　）
A、向左平移
π
4
个长度单位
B、向右平移
π
4
个长度单位
C、向左平移
π
8
个长度单位
D、向右平移
π
8
个长度单位
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由条件利用诱导公式可得y=
2
sin（x+
π
4
）=
2
cos（x-
π
4
），再根据函数y=Asin（ωx+φ）的图象变换规律，可得结论．
解答： 解：∵函数y=
2
sin（x+
π
4
）=
2
cos（
π
4
-x）=
2
cos（x-
π
4
），
∴将函数y=
2
sin（x+
π
4
）=
2
cos（x-
π
4
） 的图象向左平移
π
4
个长度单位，
可得函数y=
2
cosx的图象，
故选：A．
点评：本题主要考查诱导公式、函数y=Asin（ωx+φ）的图象变换规律，属于基础题．
练习册系列答案
相关题目
如果关于x的不等式f（x）＜0和g（x）＜0的解集分别为（a，b）和（
1
b
，
1
a
），那么称这两个不等式为对偶不等式．如果不等式x2-4
3
x•cos2θ+2＜0与不等式2x2+4x•sin2θ+1＜0为对偶不等式，且θ∈（
π
2
，π），则cosθ=
 
．
函数y=xsinx+
x
的导数是
 
．
设函数f（x）=x（ex-ae-x）为R上的偶函数，则实数a的值为
 
．
复数（i+1）i的共轭复数是（　　）
A、1+iB、1-i
C、-1+iD、-1-i
给出下列命题：
①若一个平面经过另一个平面的一条垂线，那么这两个平面相互垂直；
②若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；
③若两条平行直线中的一条垂直于直线m，那么另一条直线也与直线m垂直；
④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．
其中，是真命题的个数有（　　）
A、1B、2C、3D、4
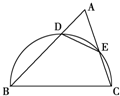如图，锐角三角形ABC中，以BC为直径的半圆分别交AB、AC于点D、E，则△ADE与△ABC的面积之比为（　　）
A、cosA
B、sinA
C、sin2A
D、cos2A
函数f（x）=
2-x-1，x≤0
lgx，x＞0
，满足f（x）＞1的x的取值范围是（　　）
A、（-1，10）
B、（-1，+∞）
C、{x|x＞10或x＜-2}
D、{x|x＞10或x＜-1}
将5名大学毕业生全部分配给3所不同的学校，不同的分配方式的种数有（　　）
A、8B、15C、125D、243

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网