题目内容
数列{an}的通项公式为an=n2+1，则a5的值为（ ）
| A、5 | B、10 | C、17 | D、26 |
考点：数列的函数特性
专题：等差数列与等比数列
分析：利用数列的通项公式求解．
解答：
解：∵为an=n2+1，
∴a5=52+1=26．
故选：D．
∴a5=52+1=26．
故选：D．
点评：本题考查数列的第5项的求法，是基础题，解题时要认真审题，注意通项公式的合理运用．
练习册系列答案
相关题目
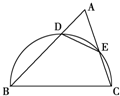如图，锐角三角形ABC中，以BC为直径的半圆分别交AB、AC于点D、E，则△ADE与△ABC的面积之比为（ ）| A、cosA |
| B、sinA |
| C、sin2A |
| D、cos2A |
甲、乙、丙等五人站成一排，要求甲、乙均不与丙相邻，则不同的排法为（ ）
| A、72 | B、36 | C、52 | D、24 |
将5名大学毕业生全部分配给3所不同的学校，不同的分配方式的种数有（ ）
| A、8 | B、15 | C、125 | D、243 |
已知正四面体A-BCD棱长都为
，M为AC中点，N为CD中点，求异面直线BM与AN所成角的余弦值（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知一条直线过点（3，-2）与点（-1，-2），则这条直线的倾斜角是（ ）
| A、0° | B、45° |
| C、60° | D、90° |
已知直线L的参数方程为
（t为参数 ），则直线的倾斜角为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
若等差数列{an}满足：
＜-1，且其前n项和Sn有最大值．则当数列Sn＞0时，n的值为（ ）
| a11 |
| a12 |
| A、20 | B、21 | C、23 | D、22 |
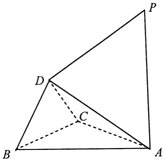已知△ABC与△DBC都是边长为2的等边三角形，且平面ABC⊥平面DBC，过点A作PA⊥平面ABC，且AP=2