题目内容
2014年某通讯公司推出一组手机卡号码,卡号的前七位数字固定,后四位数从“0000”到“9999”共10000个号码.公司规定:凡卡号的后四位带数字“5”或“8”的一律作为“金马卡”,享受一定优惠政策,则这组号码中“金马卡”的个数为( )
| A、2000 | B、4096 |
| C、5904 | D、8320 |
考点:计数原理的应用
专题:应用题,排列组合
分析:由题意知凡卡号的后四位不带数字“5”或“8”的一律不能作为“金兔卡”,后四位没有5和8,后四位中的每一个组成数字只能从另外8个中选,每一位有8种选法,根据分步计数原理得到结果,用总数减去不合题意的即可.
解答:
解:∵凡卡号的后四位带数字“5”或“8”的一律作为“金马卡”,
∴凡卡号的后四位不带数字“5”或“8”的一律不能作为“金马卡”,
后四位没有5和8,
∴后四位中的每一个组成数字只能从另外8个中选,
根据分步计数原理知共有8×8×8×8=4096,
∴符合条件的有10000-4096=5904,
故选:C.
∴凡卡号的后四位不带数字“5”或“8”的一律不能作为“金马卡”,
后四位没有5和8,
∴后四位中的每一个组成数字只能从另外8个中选,
根据分步计数原理知共有8×8×8×8=4096,
∴符合条件的有10000-4096=5904,
故选:C.
点评:本题考查分步计数原理的应用,考查带有约束条件的数字问题,这种题目若是从正面来做包括的情况比较多,可以选择从反面来解决,逆向思维解答.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
复数(i+1)i的共轭复数是( )
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
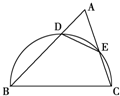 如图,锐角三角形ABC中,以BC为直径的半圆分别交AB、AC于点D、E,则△ADE与△ABC的面积之比为( )
如图,锐角三角形ABC中,以BC为直径的半圆分别交AB、AC于点D、E,则△ADE与△ABC的面积之比为( )| A、cosA |
| B、sinA |
| C、sin2A |
| D、cos2A |
有一段演绎推理是这样的“任何实数的平方都大于0,因为a∈R,所以a2>0”结论显然是错误的,是因为( )
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、非以上错误 |
函数f(x)=
,满足f(x)>1的x的取值范围是( )
|
| A、(-1,10) |
| B、(-1,+∞) |
| C、{x|x>10或x<-2} |
| D、{x|x>10或x<-1} |
下列说法正确的是( )
| A、相关指数R2越大的模型,拟合效果越好 |
| B、回归直线的斜率都大于零 |
| C、相关系数r越大,线性相关性越强 |
| D、相关系数r∈(-1,1) |
甲、乙、丙等五人站成一排,要求甲、乙均不与丙相邻,则不同的排法为( )
| A、72 | B、36 | C、52 | D、24 |
已知直线L的参数方程为
(t为参数 ),则直线的倾斜角为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|