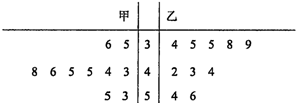
题目内容
若函数f（x）=
在区间（a-1，2a）上是单调递增函数，则实数a的取值范围为 ．
| 4x |
| x2+1 |
考点：函数单调性的性质
专题：计算题,导数的概念及应用
分析：求导数，确定函数的单调递增区间，利用条件建立不等式，即可得出结论．
解答：
解：∵f（x）=
，
∴f′（x）=
令f′（x）＞0可得-1＜x＜1，则
∵函数f（x）=
在区间（a-1，2a）上是单调递增函数，
∴-1≤a-1＜2a≤1，
∴0≤a≤
，
∴实数a的取值范围为[0，
]．
故答案为：[0，
]．
| 4x |
| x2+1 |
∴f′（x）=
| 4(1+x)(1-x) |
| (x2+1)2 |
令f′（x）＞0可得-1＜x＜1，则
∵函数f（x）=
| 4x |
| x2+1 |
∴-1≤a-1＜2a≤1，
∴0≤a≤
| 1 |
| 2 |
∴实数a的取值范围为[0，
| 1 |
| 2 |
故答案为：[0，
| 1 |
| 2 |
点评：本题考查了函数单调性的性质，考查利用导数研究函数的单调性，考查学生的计算能力，属于中档题．
练习册系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
